Question

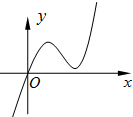g′（x）是函数g（x）=sin²（2x+

π

6

）的导函数，f′（x）是定义城为R的函数f（x）的导函数，且满足f（4）=g′（-

π

24

），又已知函数y=f′（x）的图象如图所示，若两正数a，b满足f（2a+b）＜1，则

b+2

a+2

的取值范围是

 

．

Answer 1

考点：利用导数研究函数的单调性

专题：导数的综合应用

分析：由已知推导出

a＞0 b＞0 2a+b＜4

，

b+2

a+2

表示上面不等式对应的区域内的点（a，b）和（-2，-2）连线的斜率，由此能求出

b+2

a+2

的取值范围．

解答： 解：∵g（x）=sin²（2x+

π

6

），
∴g′(x)=2sin(4x+

π

3

)，
∴f（4）=g′(-

π

24

)=2sin

π

6

=1，
由函数y=f′（x）的图象知当x＞0时，f′（x）＞0，
即函数y=f（x）在（0，+∞）上是增函数，
∴两正数a，b满足f（2a+b）＜1，
∴

a＞0 b＞0 f(2a+b)＜f(4)

，∴

a＞0 b＞0 2a+b＜4

，

b+2

a+2

表示上面不等式对应的区域内的点（a，b）和（-2，-2）连线的斜率，
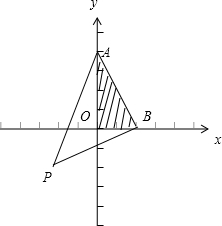
作出可行域OAB，
∵k_PB=

0+2

2+2

=

1

2

，kPA=

4+2

0+2

=3．
∴

b+2

a+2

的取值范围是（

1

2

，3）．
故答案为：（

1

2

，3）．

点评：本题考查代数式的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．