题目内容
18.定义在区间(0,$\frac{π}{2}$)上的函数y=6cosx的图象与y=5tanx的图象的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图象交于点P2,则线段P1P2的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 由题意,函数y=6cosx的图象与y=5tanx的图象的交点为P,设P的坐标(x1,y1),则有5tanx1=6cosx1,求出x1,y1,过点P作PP1⊥x轴于点P1,则x=x1,可得y2=sinx1,线段P1P2的长为y2可得答案.
解答 解:由题意,函数y=6cosx的图象与y=5tanx的图象的交点为P,设P的坐标(x1,y1),
则有5tanx1=6cosx1,
可得:5sinx1=6cos2x1,
得6sin2x1+5sinx1-6=0,即(3sinx1-2)(2sinx1+3)=0,
解得:sinx1=$\frac{2}{3}$,sinx1=$-\frac{3}{2}$(舍去)
可得y2=sinx1=$\frac{2}{3}$
∴线段P1P2的长为y2=$\frac{2}{3}$.
故选B
点评 本题考查了三角函数的图象,以及同角三角函数关系式的计算.属于中档题.

练习册系列答案
相关题目
8.按如图所示的程序框图,若输入a=81,则输出的i=( )
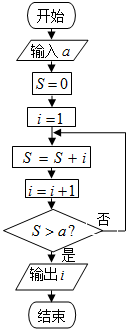

| A. | 14 | B. | 17 | C. | 19 | D. | 21 |
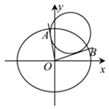 如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.
如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.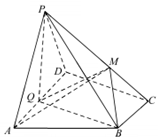 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD丄底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD,BC=$\frac{1}{2}$AD
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD丄底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD,BC=$\frac{1}{2}$AD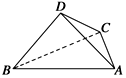 如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.