题目内容
9.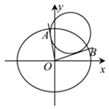 如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.
如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0,y0)是椭圆C上的动点,过原点O引两条射线l1,l2与圆M:(x-x0)2+(y-y0)2=$\frac{2}{3}$分别相切,且l1,l2的斜率k1,k2存在.
①试问k1•k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1,l2与椭圆C分别交于点A,B,求|OA|•|OB|的最大值.
分析 (Ⅰ)由c=2,求得P点坐标,代入椭圆方程,由a2-b2=1,即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)①设射线l的方程y=kx,代入椭圆方程,由韦达定理即可求得k1k2=$\frac{3{y}_{0}^{2}-2}{3{x}_{0}^{2}-2}$,由y02=1-$\frac{{x}_{0}^{2}}{2}$,即可求得k1k2=-$\frac{1}{2}$;
②方法一:分别求得直线OA及OB的方程代入椭圆方程,求得|OA|及|OB|,利用基本不等式的性质,即可求得|OA|•|OB|的最大值;
方法二:|OA|2+|OB|2=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$+$\frac{2+2{k}_{2}^{2}}{1+2{k}_{2}^{2}}$,y02=1-$\frac{{x}_{0}^{2}}{2}$,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA|•|OB|的最大值.
解答 解:(Ⅰ)由2c=2,c=1,设直线直线y=x被与椭圆C相交于P,Q两点,
则丨OP丨=$\frac{2\sqrt{3}}{3}$,设P($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),代入椭圆方程,$\frac{2}{3{a}^{2}}+\frac{2}{3{b}^{2}}=1$,①
由a2-b2=1,②
解得:a2=2,b2=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)①设射线l的方程y=kx,A(x1,y1),B(x2,y2),
由$\frac{丨k{x}_{0}-{y}_{0}丨}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{6}}{3}$,两边平方得(3x02-2)k2-6x0y0k+3y02-2=0,
由y02=1-$\frac{{x}_{0}^{2}}{2}$,
∴k1k2=$\frac{3{y}_{0}^{2}-2}{3{x}_{0}^{2}-2}$=$\frac{3(1-\frac{{x}_{0}^{2}}{2})-2}{3{x}_{0}^{2}-2}$=-$\frac{1}{2}$,
∴k1•k2为定值,定值-$\frac{1}{2}$,
②方法一:联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=2}\\{y={k}_{1}x}\end{array}\right.$,消去y,x12=$\frac{2}{1+2{k}^{2}}$,丨OA丨=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$,同理丨OA丨=$\frac{2+2{k}_{2}^{2}}{1+2{k}_{2}^{2}}$,
|OA|2•|OB|2=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$•$\frac{2+2{k}_{2}^{2}}{1+2{k}_{2}^{2}}$=4×$\frac{({k}_{1}{k}_{2})^{2}+({k}_{1}^{2}+{k}_{2}^{2})+1}{4({k}_{1}{k}_{2})^{2}+2({k}_{1}^{2}+{k}_{1}^{2})+1}$=$\frac{4({k}_{1}^{2}+{k}_{2}^{2})+5}{2({k}_{1}^{2}+{k}_{1}^{2})+2}$=2+$\frac{1}{2({k}_{1}^{2}+{k}_{1}^{2})+2}$,
=2+$\frac{1}{2{k}_{1}^{2}+\frac{1}{2{k}_{1}^{2}}+2}$≤$\frac{9}{4}$,当且仅当k12=$\frac{1}{2}$,取等号,
∴|OA|•|OB|的最大值为$\frac{3}{2}$,
方法二:联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=2}\\{y={k}_{1}x}\end{array}\right.$,消去y,x12=$\frac{2}{1+2{k}^{2}}$,丨OA丨=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$,同理丨OA丨=$\frac{2+2{k}_{2}^{2}}{1+2{k}_{2}^{2}}$,
则|OA|2+|OB|2=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$+$\frac{2+2{k}_{2}^{2}}{1+2{k}_{2}^{2}}$=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$+$\frac{2+\frac{1}{2{k}_{1}^{2}}}{1+\frac{1}{2{k}_{1}^{2}}}$=$\frac{2+2{k}_{1}^{2}}{1+2{k}_{1}^{2}}$+$\frac{1+4{k}_{1}^{2}}{1+2{k}_{1}^{2}}$=3,
由|OA|2+|OB|2≥2|OA||OB|,则|OA||OB|≤$\frac{3}{2}$,当且仅当|OA|=|OB|时,取等号,
∴|OA|•|OB|的最大值$\frac{3}{2}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,基本不等式的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
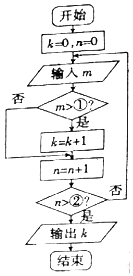 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.