题目内容
13.设Sn是等差数列{an}的前n项和,若a1>0,S8=S13,Sk=0,则k的值为21.分析 由等差数列{an}的前n项和公式能求出a1=-10d,d<0,由此能求出结果.
解答 解:∵Sn是等差数列{an}的前n项和,a1>0,S8=S13,Sk=0,
∴$\left\{\begin{array}{l}{{a}_{1}>0}\\{8{a}_{1}+\frac{8×7}{2}d=13{a}_{1}+\frac{13×12}{2}d}\end{array}\right.$,
解得a1=-10d,d<0,
∴${S}_{n}=n{a}_{1}+\frac{n(n-1)}{2}d$=-10nd+$\frac{n(n-1)}{2}d$,
∵${S}_{k}=-10kd+\frac{k(k-1)}{2}d$=0,
∴k=21.
故答案为:21.
点评 本题考查等差数列中实数值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
8.直线y=2x+m和圆x2+y2=1交于点A,B,以x轴的正方向为始边,OA为终边(O是坐标原点)的角为α,OB为终边的角为β,若|AB|=$\sqrt{3}$,那么sin(α-β)的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $±\frac{1}{2}$ | D. | $±\frac{{\sqrt{3}}}{2}$ |
2.设a=20.2,b=ln2,c=log2$\frac{9}{10}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
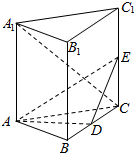 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠ABC=$\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠ABC=$\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点. 如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.