题目内容
若一个圆锥的轴截面是等边三角形，其面积为
，则这个圆锥的体积为（ ）
| 3 |
| A、3π | ||||
B、
| ||||
C、
| ||||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由圆锥的轴截面是等边三角形及面积，分析圆锥的母线长和底面半径长，进而求出圆锥的高，结合圆锥的体积公式即可获得问题的解答．
解答：
解：由题意：圆锥的轴截面是边长为a的等边三角形，其面积为
，
∴对于轴截面有：
a2=
，
∴a2=4，
∴a=2，
故圆锥的母线l=2，底面半径r=1，
则圆锥的高h=
=
．
故圆锥的体积V=
πr2h=
π，
故选：B
| 3 |
∴对于轴截面有：
| ||
| 4 |
| 3 |
∴a2=4，
∴a=2，
故圆锥的母线l=2，底面半径r=1，
则圆锥的高h=
| l2-r2 |
| 3 |
故圆锥的体积V=
| 1 |
| 3 |
| ||
| 3 |
故选：B
点评：本题考查的是圆锥的体积求解问题．在解答的过程当中充分体现了三角形面积公式的应用、圆锥体积公式的应用以及转化思想的应用．值得同学们体会反思．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
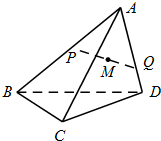如图，在三棱锥A-BCD中，三条侧棱AB，AC，AD两两垂直，AB=AC=AD=6，P，Q分别是侧面ABC和棱AD上动点，PQ=4，M为线段PQ中点，当P，Q运动时，点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于已知两条直线m，n，两个平面α，β，下面四个命题错误的是（ ）
| A、m⊥α，α⊥β⇒m∥β |
| B、m⊥α，m⊥n⇒n∥α或n?α |
| C、m⊥α，n∥α⇒m⊥n |
| D、α⊥β，m⊥β，m?α⇒m∥α． |