题目内容
已知两定点M(－1,0)，N(1,0)，若直线上存在点P，使|PM|＋|PN|＝4，则该直线为“A型直线”．给出下列直线，其中是“A型直线”的是________(填序号)．
①y＝x＋1；②y＝2；③y＝－x＋3；④y＝－2x＋3.
①④
[解析] 由题意可知，点P的轨迹是以M，N为焦点的椭圆，其方程是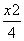
＋
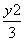＝1，
①把y＝x＋1代入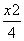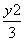＋＝1并整理得，7x2＋8x－8＝0，
∵Δ＝82－4×7×(－8)>0，直线与椭圆有两个交点，
∴y＝x＋1是“A型直线”．
②把y＝2代入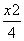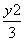＋＝1，得＝－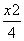
不成立，直线与椭圆无交点，∴y＝2不是“A型直线”．
③把y＝－x＋3代入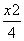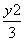＋＝1并整理得，7x2－24x＋24＝0，Δ＝(－24)2－4×7×24<0，∴y＝－x＋3不是“A型直线”．
④把y＝－2x＋3代入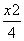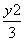＋＝1并整理得，19x2－48x＋24＝0，∵Δ＝(－48)2－4×19×24>0，∴y＝－2x＋3是“A型直线”．
练习册系列答案
相关题目
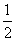＝0能围成三角形，则k不等于________．
＋
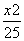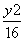＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点距离为________．
，
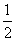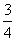] B．[
，
＋
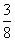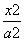＝1(a>b>0)的两焦点，P是椭圆上任一点，过一焦点引∠F1PF2的外角平分线的垂线，则垂足Q的轨迹为( )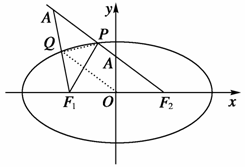
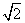，在y轴上截得线段长为2
.
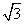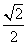，求圆P的方程．