题目内容
椭圆C: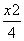 +
+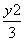 =1的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[-2,-1],那么直线PA1斜率的取值范围是( )
=1的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[-2,-1],那么直线PA1斜率的取值范围是( )
A.[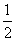 ,
,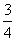 ] B.[
] B.[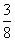 ,
,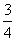 ]
]
C.[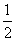 ,1] D.[
,1] D.[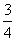 ,1]
,1]
B
[解析]

如图:A1(-2,0),A2(2,0)
直线A2M的方程为y=-(x-2),即y=2-x,
代入椭圆方程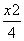 +
+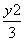 =1中消去y得,7x2-16x+4=0,
=1中消去y得,7x2-16x+4=0,
∴2+x= ,∴x=
,∴x= ,∴M点坐标为(
,∴M点坐标为( ,
, ).
).
同理可得N点坐标为( ,
, )
)
∵kA1M=
∴直线PA1斜率的取值范围是[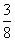 ,
,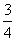 ].
].
[解法探究] 点P在椭圆C上运动,PA2的斜率取值已知,求PA1的斜率的取值范围,若能找到kPA1与kPA2的关系,则解答更简便.
由条件知,A1(-2,0),A2(2,0),
 ∴kPA1=
∴kPA1= ,
,
∵-2≤kPA2≤-1,∴4≤-4kPA2≤8,∴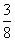 ≤kPA1≤
≤kPA1≤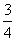 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ) B.(0,
) B.(0,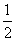 ,1) D.(0,1]
,1) D.(0,1]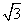 y-2
y-2 =( )
=( )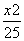 +
+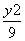 =1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )
=1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( )
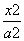 +
+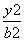 =1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为
=1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为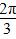 时,此椭圆的离心率是________.
时,此椭圆的离心率是________.