题目内容
过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线C交于A、B两点,当点A的纵坐标为1时,|AF|=2.
(1)求抛物线C的方程;
(2)若直线l的斜率为2,问抛物线C上是否存在一点M,使得MA⊥MB,并说明理由.
(1)由抛物线的定义得|AF|等于点A到准线y=- 的距离,
的距离,
∴1+ =2,∴p=2,
=2,∴p=2,
∴抛物线C的方程为x2=4y.

(2)抛物线C的焦点为F(0,1),直线l的方程y=2x+1,
设点A、B、M的坐标分别为(x1, )、(x2,
)、(x2, )、(x0,
)、(x0, ),
),
由方程组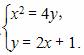 消去y得,x2=4(2x+1),
消去y得,x2=4(2x+1),
即x2-8x-4=0,
由韦达定理得x1+x2=8,x1x2=-4.
 ∴(x1-x0)(x2-x0)+
∴(x1-x0)(x2-x0)+ (x1-x0)(x2-x0)(x1+x0)(x2+x0)=0.
(x1-x0)(x2-x0)(x1+x0)(x2+x0)=0.
∵M不与A,B重合,∴(x1-x0)(x2-x0)≠0,
∴1+ (x1+x0)(x2+x0)=0,x1x2+(x1+x2)x0+x
(x1+x0)(x2+x0)=0,x1x2+(x1+x2)x0+x +16=0,
+16=0,
∴x +8x0+12=0,∵Δ=64-48>0.
+8x0+12=0,∵Δ=64-48>0.
∴方程x +8x0+12=0有解,即抛物线C上存在一点M,使得MA⊥MB.
+8x0+12=0有解,即抛物线C上存在一点M,使得MA⊥MB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 则实数
则实数 的值是( )
的值是( ) B. 2 C.
B. 2 C.  D. 4
D. 4  =1(x>1) B.x2-
=1(x>1) B.x2-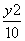 =1(x>0)
=1(x>0)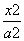 +
+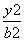 =1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为
=1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为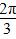 时,此椭圆的离心率是________.
时,此椭圆的离心率是________.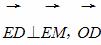 =(0,-8),N在y轴上,且
=(0,-8),N在y轴上,且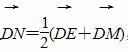 点E在x轴上移动.
点E在x轴上移动.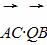 的最小值.
的最小值.
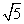 ,则它的渐近线方程为( )
,则它的渐近线方程为( )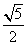 x
x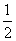 x D.y=±
x D.y=±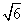 x
x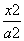 -y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则
-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则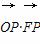 的取值范围为( )
的取值范围为( )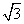 ,+∞) B.[3+2
,+∞) B.[3+2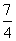 ,+∞) D.[
,+∞) D.[ -1)=0表示的曲线是( )
-1)=0表示的曲线是( )