题目内容
设集合P={x|2x2-5x-12≤0}，Q={x|（x-2a）（a-x）＞0}，若P∩Q=∅，求实数a的取值范围．
考点：交集及其运算
专题：不等式的解法及应用,集合
分析：首先化简各集合，其中集合Q需要讨论a的符号，然后由题意得到集合端点的关系．
解答：
解：由已知P={x|-1.5≤x≤4}，
①a=0时，Q=∅，满足P∩Q=∅；
②a＞0时，Q={x|a＜x＜2a}，要使P∩Q=∅，只要a≥4并且2a≤-1.5，所以a≥4；
③a＜0时，Q={x|2a≤x≤a}，要使P∩Q=∅，只要a≤-1.5；
综上实数a的取值范围是a=0或a≥4，或a≤-1.5．
①a=0时，Q=∅，满足P∩Q=∅；
②a＞0时，Q={x|a＜x＜2a}，要使P∩Q=∅，只要a≥4并且2a≤-1.5，所以a≥4；
③a＜0时，Q={x|2a≤x≤a}，要使P∩Q=∅，只要a≤-1.5；
综上实数a的取值范围是a=0或a≥4，或a≤-1.5．
点评：本题考查的知识点是集合的交集及其运算，以及讨论的思想解二次不等式，属于中档题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
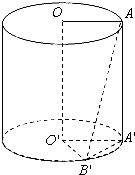圆柱的高为4cm，底面半径为3cm，上底面一条半径OA与下底面一条半径O′B′成60°角，求：