题目内容
讨论函数f(x)=alnx+
ax2-x(a∈R)的单调性.
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:通过讨论a的范围,结合二次函数的性质,从而得出函数的单调区间.
解答:
解:(1)a=0时,f(x)=-x,∴f(x)在(0,+∞)递减;
(2)a≠0时,f′(x)=
+ax-1=
,(x>0),
令g(x)=ax2-x+a,
①0<a<
时,△=1-4a2>0,x=
,
∴在区间(0,
)和(
,+∞)上,g(x)>0,f′(x)>0,f(x)递增,
在区间(
,
,)上,g(x)<0,f′(x)<0,f(x)递减,
②a≥
时,△≤0,g(x)≥0,f′(x)≥0,f(x)在(0,+∞)递增,
③-
<a<0时,△=1-4a2>0,x=
,
∴在区间(0,
)和(
,+∞)上,g(x)<0,f′(x)<0,f(x)递减,
在区间(
,
,)上,g(x)>0,f′(x)>0,f(x)递增,
④a≤-
时,△≤0,g(x)≤0,f′(x)≤0,f(x)在(0,+∞)递减.
(2)a≠0时,f′(x)=
| a |
| x |
| ax2-x+a |
| x |
令g(x)=ax2-x+a,
①0<a<
| ||
| 2 |
1±
| ||
| 2a |
∴在区间(0,
1-
| ||
| 2a |
1+
| ||
| 2a |
在区间(
1-
| ||
| 2a |
1+
| ||
| 2a |
②a≥
| ||
| 2 |
③-
| ||
| 2 |
1±
| ||
| 2a |
∴在区间(0,
1-
| ||
| 2a |
1+
| ||
| 2a |
在区间(
1-
| ||
| 2a |
1+
| ||
| 2a |
④a≤-
| ||
| 2 |
点评:本题考查了函数的单调性,二次函数的性质,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
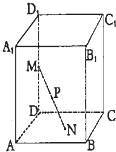 已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
有穷数列1,23,26,29,…,23n+6的项数是( )
| A、3n+7 | B、3n+6 |
| C、n+3 | D、n+2 |
 如图,矩形ABCD,点A,B分别在x正半轴和y正半轴上,点C,D在第一象限内|
如图,矩形ABCD,点A,B分别在x正半轴和y正半轴上,点C,D在第一象限内|