题目内容
若双曲线
-
=1(a>0)的离心率为2,则a= .
| x2 |
| a2 |
| y2 |
| 9 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:运用离心率公式,可得c=2a,结合c2=a2+b2,解方程即可得到a.
解答:
解:双曲线
-
=1(a>0)的离心率为2,
则e=
=2,即c2=4a2=a2+9,
解得a=
,
故答案为:
.
| x2 |
| a2 |
| y2 |
| 9 |
则e=
| c |
| a |
解得a=
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的方程和性质,考查离心率的求法,属于基础题.

练习册系列答案
相关题目
平面向量
,
满足|
|=2,|
+
|=4,且向量
与向量
+
的夹角为
,则|
|为( )
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| π |
| 3 |
| b |
| A、2 | ||||
B、2
| ||||
C、2
| ||||
D、2
|
如图所示程序框图,其功能是输入x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
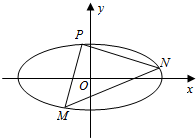 如图,椭圆C:
如图,椭圆C: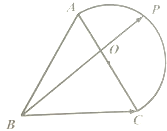 已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则
已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则