题目内容
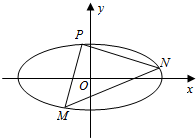 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P,M,N椭圆C上的三个动点.
(i)若直线MN过点D(0,-
| 1 |
| 2 |
(ii)试探究:是否存在△PMN是以O为中心的等边三角形,若存在,请给出证明;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用离心率以及短轴长,求出椭圆中a、b、c.即可求椭圆C的方程;
(Ⅱ)(i)由已知,直线MN的斜率存在,设直线MN方程为y=kx-
,M(x1,y1),N(x2,y2).
联立直线与椭圆方程,利用韦达定理,一弦长公式,推出面积S△PMN的表达式,通过换元,利用导数求出面积的最大值.
(ii)假设存在△PMN是以O为中心的等边三角形.
(1)当P在y轴上时,推出与△PMN为等边三角形矛盾.
(2)当P在x轴上时,同理推出与△PMN为等边三角形矛盾.
(3)当P不在坐标轴时,设P(x0,y0),MN的中点为Q,则kOP=
,通过O为△PMN的中心,则得到Q(-
,-
).设M(x1,y1),N(x2,y2),推出kMN,说明kOP•kMN=
•(-
•
)=-
≠-1,因此OP与MN不垂直,与等边△PMN矛盾,得到不存在△PMN是以O为中心的等边三角形.
(Ⅱ)(i)由已知,直线MN的斜率存在,设直线MN方程为y=kx-
| 1 |
| 2 |
联立直线与椭圆方程,利用韦达定理,一弦长公式,推出面积S△PMN的表达式,通过换元,利用导数求出面积的最大值.
(ii)假设存在△PMN是以O为中心的等边三角形.
(1)当P在y轴上时,推出与△PMN为等边三角形矛盾.
(2)当P在x轴上时,同理推出与△PMN为等边三角形矛盾.
(3)当P不在坐标轴时,设P(x0,y0),MN的中点为Q,则kOP=
| x0 |
| y0 |
| x0 |
| 2 |
| y0 |
| 2 |
| x0 |
| y0 |
| 1 |
| 4 |
| x0 |
| y0 |
| 1 |
| 4 |
解答:
解:(Ⅰ)由题意得
解得a=2,b=1,
所以椭圆方程为
+y2=1.
(Ⅱ)(i)由已知,直线MN的斜率存在,
设直线MN方程为y=kx-
,M(x1,y1),N(x2,y2).
由
得(1+4k2)x2-4kx-3=0,
∴x1+x2=
,x1x2=
,
又|PD|=
.
所以S△PMN=
|PD|•|x1-x2|=
=
=
.
令t=
,则t≥
,k2=
所以S△PMN=
=
=
,
令h(t)=t+
,t∈[
,+∞),则h′(t)=1-
=
>0,所以h(t)在[
,+∞),单调递增,
则t=
,即k=0时,h(t)的最小值,为h(
)=
,
所以△PMN面积的最大值为
.
(ii)假设存在△PMN是以O为中心的等边三角形.
(1)当P在y轴上时,P的坐标为(0,1),则M,N关于y轴对称,MN的中点Q在y轴上.
又O为△PMN的中心,所以
=2
,可知Q(0,-
),M(-
,-
),N(
,-
).
从而|MN|=2
,|PM|=
,|MN|≠|PM|,与△PMN为等边三角形矛盾.
(2)当P在x轴上时,同理可知,|MN|≠|PM|,与△PMN为等边三角形矛盾.
(3)当P不在坐标轴时,设P(x0,y0),MN的中点为Q,则kOP=
,
又O为△PMN的中心,则
=2
,可知Q(-
,-
).
设M(x1,y1),N(x2,y2),则x1+x2=2xQ=-x0,y1+y2=2yQ=-y0,
又x12+4y12=4,x22+4y22=4,两式相减得kMN=
=-
=-
•
=-
•
,
从而kMN=-
•
.
所以kOP•kMN=
•(-
•
)=-
≠-1,
所以OP与MN不垂直,与等边△PMN矛盾.
综上所述,不存在△PMN是以O为中心的等边三角形.
|
所以椭圆方程为
| x2 |
| 4 |
(Ⅱ)(i)由已知,直线MN的斜率存在,
设直线MN方程为y=kx-
| 1 |
| 2 |
由
|
∴x1+x2=
| 4k |
| 1+4k2 |
| -3 |
| 1+4k2 |
又|PD|=
| 3 |
| 2 |
所以S△PMN=
| 1 |
| 2 |
| 3 |
| 4 |
| (x1+x2)2-4x1x2 |
=
| 3 |
| 4 |
|
3
| ||
| 2(1+4k2) |
令t=
| 16k2+3 |
| 3 |
| t2-3 |
| 16 |
所以S△PMN=
| 3t | ||
2(1+4•
|
| 6t |
| t2+1 |
| 6 | ||
t+
|
令h(t)=t+
| 1 |
| t |
| 3 |
| 1 |
| t2 |
| t2-1 |
| t2 |
| 3 |
则t=
| 3 |
| 3 |
4
| ||
| 3 |
所以△PMN面积的最大值为
3
| ||
| 2 |
(ii)假设存在△PMN是以O为中心的等边三角形.
(1)当P在y轴上时,P的坐标为(0,1),则M,N关于y轴对称,MN的中点Q在y轴上.
又O为△PMN的中心,所以
| PO |
| OQ |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
从而|MN|=2
| 3 |
| ||
| 2 |
(2)当P在x轴上时,同理可知,|MN|≠|PM|,与△PMN为等边三角形矛盾.
(3)当P不在坐标轴时,设P(x0,y0),MN的中点为Q,则kOP=
| x0 |
| y0 |
又O为△PMN的中心,则
| PO |
| OQ |
| x0 |
| 2 |
| y0 |
| 2 |
设M(x1,y1),N(x2,y2),则x1+x2=2xQ=-x0,y1+y2=2yQ=-y0,
又x12+4y12=4,x22+4y22=4,两式相减得kMN=
| y1-y2 |
| x1-x2 |
| 1 |
| 4 |
| x1+x2 |
| y1+y2 |
| 1 |
| 4 |
| x1+x2 |
| y1+y2 |
| 1 |
| 4 |
| x0 |
| y0 |
从而kMN=-
| 1 |
| 4 |
| x0 |
| y0 |
所以kOP•kMN=
| x0 |
| y0 |
| 1 |
| 4 |
| x0 |
| y0 |
| 1 |
| 4 |
所以OP与MN不垂直,与等边△PMN矛盾.
综上所述,不存在△PMN是以O为中心的等边三角形.
点评:本小题考查点到直线的距离公式、椭圆的性质、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力、分析解决问题能力,考查函数与方程思想、数形结合思想、特殊与一般思想、化归与转化思想

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义运算a*b,a*b
,例如1*2=1,已知函数f(x)=1*ax(0<a<1)且f(4)=
,则f(2)=( )
|
| 1 |
| 2014 |
| A、-1007 | ||||
| B、-1006 | ||||
| C、1007 | ||||
D、
|
如图是一个四棱锥在空间直角坐标系xoz、xoy、yoz三个平面上的正投影,则此四棱锥的体积为( )
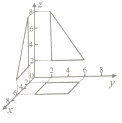

| A、94 | B、32 | C、64 | D、16 |

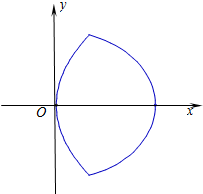 如图,曲线E是由抛物线弧E1:y2=4x(0≤x≤
如图,曲线E是由抛物线弧E1:y2=4x(0≤x≤
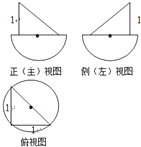 有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).
有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).