题目内容

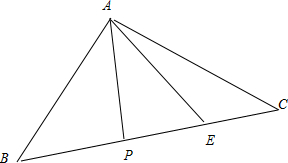
已知三角形ABC中，AB=AC，BC=4，∠BAC=120°，
BE
=3
EC
，若P是BC边上的动点，则
AP
•
AE
的取值范围是
 
．
考点：平面向量数量积的运算
专题：函数的性质及应用
分析：运图形得出
AB
•
BC
=
4
3
×4×（-
3
2
）=-8，
BE
=
3
BC
4
，
BP
=λ
BC
，0≤λ≤1化简得出
AP
•
AE
=（
AB
+
BP
）•(
AB
+BE)=
.
AB
2+λ
BC•
AB
+
3λ
4
BC
2+3×
AB
•
BC
4
，运用数量积求解即可．
解答： 解：∵三角形ABC中，AB=AC，BC=4，∠BAC=120°
∴AB=
4
3
，∠ABC=30°，
求出
AB
•
BC
=
4
3
×4×（-
3
2
）=-8，
∵
BE
=3
EC
，
∴
BE
=
3
BC
4
，
BP
=λ
BC
，0≤λ≤1
∵
AP
•
AE
=（
AB
+
BP
）•(
AB
+BE)=
.
AB
2+λ
BC•
AB
+
3λ
4
BC
2+3×
AB
•
BC
4

∴
AP
•
AE
=
16
3
-8λ+12λ+
3
4
×（-8）=4λ-
2
3
，0≤λ≤1
根据单调性得出：
AP
•
AE
的取值范围-
2
3
≤λ≤
10
3
，
故答案为：[-
2
3
，
10
3
]

点评：本题考查了平面向量的运用算，向量的分解合成，数量积的运用，属于中档题，关键是转化为统一的向量求解．
练习册系列答案
相关题目
设集合A=[0，1），B=[1，2]，函数f（x）=
2x，(x∈A)
4-2x，(x∈B)
，x0∈A，且f[f（x0）]∈A，则x0 的取值范围是（　　）
A、（
2
3
，1）
B、[0，
3
4
]
C、（log2
3
2
，1）
D、（log32，1）
定义运算a*b，a*b
a，a≤b
b，a＞b
，例如1*2=1，已知函数f（x）=1*ax（0＜a＜1）且f（4）=
1
2014
，则f（2）=（　　）
A、-1007
B、-1006
C、1007
D、
1
2014
如图（1），在边长为2的正方形ABCD中，E是边AB的中点．将△ADE沿DE折起使得平面ADE⊥平面BCDE，如图（2），F是折叠后AC的中点．

（Ⅰ）求证：BF∥平面ADE；
（Ⅱ）求二面角E-AB-D的平面角的余弦值．
在△ABC中，若|
AB
|=2，|
AC
|=3，∠BAC=60°，则
BA
•
BC
=
 
．
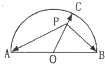如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则（
PA
+
PB
）•
PC
的最小值为（　　）
A、
9
2
B、9
C、-
9
2
D、-9
某几何体的三视图如图所示，则该几何体的体积为
 
．
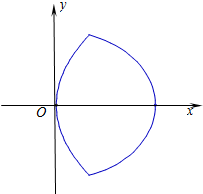如图，曲线E是由抛物线弧E1：y2=4x（0≤x≤
2
3
）与椭圆弧E2：
x2
a2
+
y2
b2
=1（
2
3
≤x≤a）所围成的封闭曲线，且E1与E2有相同的焦点．
（Ⅰ）求椭圆弧E2的方程；
（Ⅱ）设过点F（1，0）的直线与曲线E交于A，B两点，|FA|=r1，|FB|=r2，且∠AFx=α（0≤α≤π），试用cosα表示r1；并求
r1
r2
的取值范围．
若双曲线
x2
a2
-
y2
9
=1（a＞0）的离心率为2，则a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网