题目内容

平面向量
a
，
b
满足|
a
|=2，|
a
+
b
|=4，且向量
a
与向量
a
+
b
的夹角为
π
3
，则|
b
|为（　　）
A、2
B、2
3
C、2
5
D、2
5-2
3
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义可得
a
•（
a
+
b
）=4，再由向量的平方即为模的平方，计算可得|
b
|．
解答： 解：由于|
a
|=2，|
a
+
b
|=4，且向量
a
与向量
a
+
b
的夹角为
π
3
，
则
a
•（
a
+
b
）=|
a
|•|
a
+
b
|•cos
π
3
=2×4×
1
2
=4，
即有
a
2+
a
•
b
=4，即4+
a
•
b
=4，
即为
a
•
b
=0，
又（
a
+
b
）2=
a
2+
b
2+2
a
•
b
=16，
即4+|
b
|2=16，
可得|
b
|=2
3
．
故选B．
点评：本题考查向量的数量积的定义和性质，主要考查向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
相关题目
在△ABC中，若|
AB
|=2，|
AC
|=3，∠BAC=60°，则
BA
•
BC
=
 
．
如图是一个正四面体的主视图，则该四面体的高为
 
．
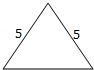
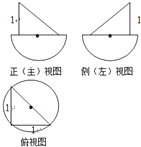有100件规格相同的铁件（铁的密度是7.8g/cm3），该铁件的三视图如图所示，其中正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成（图中单位cm）．
（1）指出该几何体的形状特征；
（2）根据图中的数据，求出此几何体的体积；
（3）问这100件铁件的质量大约有多重（π取3.1，
2
取1.4）？
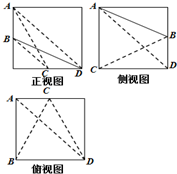在棱长为2的正方体内有一四面体A-BCD，其中B，C分别为正方体两条棱的中点，其三视图如图所示，则四面体A-BCD的体积为（　　）
A、
8
3
B、2
C、
4
3
D、1
若双曲线
x2
a2
-
y2
9
=1（a＞0）的离心率为2，则a=
 
．
用向量方法证明：已知四面体ABCD，若AB⊥CD，AD⊥BC，则AC⊥BD．
若向量
a
=（1，-2），
b
=（-3，y），且
a
∥
b
，则|
a
+
b
|=
 
．
抛物线C1：x2=2y的焦点为F，以F为圆心C2交C1于A，B两点，交C1准线于C，D两点，若四边形ABCD是矩形，则C2的标准方程为（　　）
A、x2+（y-
1
2
）2=4
B、（x-
1
2
）2+y2=4
C、x2+（y-
1
2
）2=2
D、（x-
1
2
）2+y2=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网