题目内容
在△ABC中,BC=3,CA=4,AB=5,M是边AB上的动点(含A,B两个端点).若
=λ
+μ
(λ,μ∈R),则|λ
-μ
|的取值范围是 .
| CM |
| CA |
| CB |
| CA |
| CB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,由已知可得∠C=90°.斜边AB上的高h=
.而
=λ
+μ
=(3μ,4λ),可得|
|=
∈[
,4].即可得出|λ
-μ
|=
.
| 12 |
| 5 |
| CM |
| CA |
| CB |
| CM |
| 9μ2+16λ2 |
| 12 |
| 5 |
| CA |
| CB |
| 9μ2+16λ2 |
解答:
解:如图所示,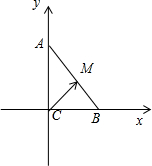
∵BC=3,CA=4,AB=5,32+42=52,
∴∠C=90°.
∴斜边AB上的高h=
.
∵
=λ
+μ
=λ(0,4)+μ(3,0)=(3μ,4λ),
∴|
|=
∈[
,4].
∵λ
-μ
=λ(0,4)-μ(3,0)=(-3μ,4λ).
则|λ
-μ
|=
∈[
,4].
故答案为:[
,4].

∵BC=3,CA=4,AB=5,32+42=52,
∴∠C=90°.
∴斜边AB上的高h=
| 12 |
| 5 |
∵
| CM |
| CA |
| CB |
∴|
| CM |
| 9μ2+16λ2 |
| 12 |
| 5 |
∵λ
| CA |
| CB |
则|λ
| CA |
| CB |
| 9μ2+16λ2 |
| 12 |
| 5 |
故答案为:[
| 12 |
| 5 |
点评:本题考查了向量坐标运算、数量积运算性质、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
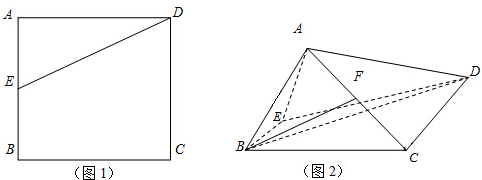
已知正四面体ABCD的棱长为a.点E,F分别是棱AC,BD的中点,则
•
的值是( )
| AE |
| AF |
| A、a2 | ||||
B、
| ||||
C、
| ||||
D、
|
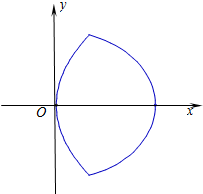 如图,曲线E是由抛物线弧E1:y2=4x(0≤x≤
如图,曲线E是由抛物线弧E1:y2=4x(0≤x≤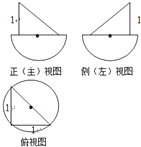 有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).
有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm). 在面积为2的平行四边形ABCD中,点P为直线AD上的动点,则
在面积为2的平行四边形ABCD中,点P为直线AD上的动点,则