题目内容
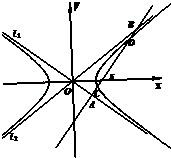 双曲线
双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| AB |
| OB |
| BF |
| FA |
(1)求双曲线的离心率;
(2)若直线AB被双曲线截得的弦长为
| 8 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设实轴长为2a,虚轴长为2b,令∠AOF=α,则由题意知tanα=
,△AOB中,∠AOB=180°-2α,tan∠AOB=-tan2α=
,由此推导出-tan2α=-
=
=
=
,从而能求出离心率.
(2)由(1)设双曲线方程为:
-
=1,直线AB的方程为:y=2x-2
m,由
,得:15x2-32
mx+84m2=0,由此利用弦长公式能求出双曲线方程.
| b |
| a |
| AB |
| OA |
| 2tanα |
| 1-tan2α |
| AB |
| OA |
| m | ||
|
| 4 |
| 3 |
(2)由(1)设双曲线方程为:
| x2 |
| 4m2 |
| y2 |
| m2 |
| 5 |
|
| 5 |
解答:
解:(1)如图,设实轴长为2a,虚轴长为2b,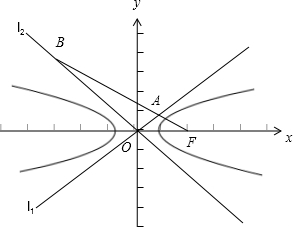
令∠AOF=α,则由题意知tanα=
,
△AOB中,∠AOB=180°-2α,tan∠AOB=-tan2α=
,
∵|
|、|
|、|
|成等差数列,
∴设|
|=m-d、|
|=m、|
|=m+d,
∵OA⊥BF,∴(m-d)2+m2=(m+d)2,
整理,得d=
m,
∴-tan2α=-
=
=
=
,
解得
=2或
=-
(舍),
∴b=2a,c=
=
a,
∴e=
=
.
(2)由(1)设双曲线方程为:
-
=1,
∵直线AB垂直于l1,故直线AB的方程为:y=2x-2
m,
由
,得:15x2-32
mx+84m2=0,
设A(x1,x2),B(x2,y2),则x1+x2=
,x1x2=
,
∵直线AB被双曲线截得的弦长为
,
∴
=
,解得m=2,
∴双曲线方程为
-
=1.

令∠AOF=α,则由题意知tanα=
| b |
| a |
△AOB中,∠AOB=180°-2α,tan∠AOB=-tan2α=
| AB |
| OA |
∵|
| OA |
| AB |
| OB |
∴设|
| OA |
| AB |
| OB |
∵OA⊥BF,∴(m-d)2+m2=(m+d)2,
整理,得d=
| 1 |
| 4 |
∴-tan2α=-
| 2tanα |
| 1-tan2α |
| AB |
| OA |
| m | ||
|
| 4 |
| 3 |
解得
| b |
| a |
| b |
| a |
| 1 |
| 2 |
∴b=2a,c=
| 4a2+a2 |
| 5 |
∴e=
| c |
| a |
| 5 |
(2)由(1)设双曲线方程为:
| x2 |
| 4m2 |
| y2 |
| m2 |
∵直线AB垂直于l1,故直线AB的方程为:y=2x-2
| 5 |
由
|
| 5 |
设A(x1,x2),B(x2,y2),则x1+x2=
32
| ||
| 15 |
| 84m |
| 15 |
∵直线AB被双曲线截得的弦长为
| 8 |
| 3 |
∴
(1+4)[(
|
| 8 |
| 3 |
∴双曲线方程为
| x2 |
| 16 |
| y2 |
| 4 |
点评:本题考查双曲线的离心率和双曲线方程的求法,解题时要认真审题,注意椭圆弦长公式的灵活运用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
函数f(x)=x-1的零点是( )
| A、0 | B、1 |
| C、(0,0) | D、(1,0) |
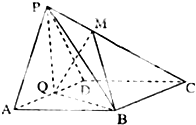 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD;
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD;  如图,在空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点.
如图,在空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点.