题目内容
6.(1)解不等式3${P}_{x}^{3}$≤2${P}_{x+1}^{2}$+6${P}_{x}^{2}$;(2)已知$\frac{1}{{C}_{5}^{m}}$-$\frac{1}{{C}_{6}^{m}}$=$\frac{7}{10{C}_{7}^{m}}$,求${C}_{8}^{m}$.
分析 (1)根据排列数公式化简不等式3${P}_{x}^{3}$≤2${P}_{x+1}^{2}$+6${P}_{x}^{2}$,求出不等式的解集即可;
(2)根据组合数公式化简$\frac{1}{{C}_{5}^{m}}$-$\frac{1}{{C}_{6}^{m}}$=$\frac{7}{10{C}_{7}^{m}}$,求出m的值,计算${C}_{8}^{m}$的值.
解答 解:(1)不等式3${P}_{x}^{3}$≤2${P}_{x+1}^{2}$+6${P}_{x}^{2}$化为
3x(x-1)(x-2)≤2(x+1)x+6x(x-1),-------(1分)
∵x≥3,
∴3(x-1)(x-2)≤2(x+1)+6(x-1),
即3x2-17x+10≤0,-------(2分)
解得$\frac{2}{3}$≤x≤5;-------(3分)
∵x≥3,且x∈N*,-------(4分)
∴不等式的解集为{3,4,5};-------(5分)
(2)$\frac{1}{{C}_{5}^{m}}$-$\frac{1}{{C}_{6}^{m}}$=$\frac{7}{10{C}_{7}^{m}}$,
∴$\frac{(5-m)!×m!}{5!}$-$\frac{(6-m)!×m!}{6!}$=$\frac{7}{10}$×$\frac{(7-m)!×m!}{7!}$,--------(2分)
化简得,1-$\frac{6-m}{6}$=$\frac{(7-m)(6-m)}{60}$,--------(3分)
解得m=2;--------(4分)
∴${C}_{8}^{m}$=${C}_{8}^{2}$=$\frac{8×7}{2}$=28.--------(5分)
点评 本题考查了排列数与组合数公式的应用问题,是基础题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | (1,2] | B. | (1,2) | C. | [2,+∞) | D. | [1,+∞) |
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | b<c<a |
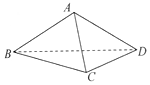 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,直线AC与底面BCD所成角的大小为( )