题目内容
11.已知不等式$\sqrt{1-{x^2}}>x+b$在$[{-1,\frac{1}{2}})$上恒成立,则b的取值范围是(-∞,0).分析 设x=sinθ,则θ∈[-$\frac{π}{2}$,$\frac{π}{6}$),则不等式$\sqrt{1-{x^2}}>x+b$在$[{-1,\frac{1}{2}})$上恒成立,转化为b<$\sqrt{2}$cos(θ+$\frac{π}{4}$),根据三角函数的性质即可求出.
解答 解:设x=sinθ,则θ∈[-$\frac{π}{2}$,$\frac{π}{6}$),
∵不等式$\sqrt{1-{x^2}}>x+b$在$[{-1,\frac{1}{2}})$上恒成立,
∴cosθ>sinθ+b在[-$\frac{π}{2}$,$\frac{π}{6}$)上恒成立,
∴b<cosθ-sinθ=$\sqrt{2}$cos(θ+$\frac{π}{4}$),
∵θ∈[-$\frac{π}{2}$,$\frac{π}{6}$),
∴θ+$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{5π}{12}$),
∴0≤cos(θ+$\frac{π}{4}$)≤$\frac{\sqrt{2}}{2}$,
∴b<0,
故b的取值范围是(-∞,0),
故选:(-∞,0)
点评 本题了不等式恒成立的问题,关键是换元,利用三角函数的性质,属于中档题

练习册系列答案
相关题目
19.已知M (-2,0),N (2,0),则以MN为直径的圆的方程是( )
| A. | x2+y2=2 | B. | x2+y2=1 | C. | x2+y2=3 | D. | x2+y2=4 |
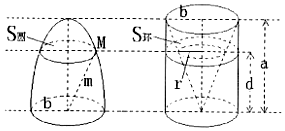 已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.
已知两个等高的几何体在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.则短轴长为4cm,长轴为6cm的椭球体的体积为16πcm3.