题目内容
17.已知数列{an}的前项和为an+2=an+1-an,且a1=2,a2=3,Sn为数列{an}的前n项和,则S2017的值为( )| A. | 0 | B. | 2 | C. | 5 | D. | 6 |
分析 an+2=an+1-an,且a1=2,a2=3,可得an+6=an.即可得出.
解答 解:∵an+2=an+1-an,且a1=2,a2=3,
∴a3=3-2=1,a4=-2,a5=-3,a6=-1,a7=2,a8=3,….
∴an+6=an.
则S2017=(a1+a2+…+a6)×336+a1=0+2=2.
故选:B.
点评 本题考查了数列的周期性、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
10.在等比数列{an}中,设a2=3,a5=81,bn=log3an,则数列{bn}的前n项和Sn为( )
| A. | $\frac{{{n^2}-n}}{2}$ | B. | $\frac{n^2}{2}$ | C. | $\frac{{{n^2}+n}}{2}$ | D. | $\frac{{{n^2}+2n}}{2}$ |
9.已知M(4,2)是直线l被椭圆x2+4y2=36所截得的线段AB的中点,则直线l的方程为( )
| A. | 2x+y-8=0 | B. | x+2y-8=0 | C. | x-2y-8=0 | D. | 2x-y-8=0 |
6.函数f(x)=2sin(2x+$\frac{π}{6}$)的图象为M,则下列结论中正确的是( )
| A. | 图象M关于直线x=-$\frac{π}{12}$对称 | |
| B. | 由y=2sin2x的图象向左平移$\frac{π}{6}$得到M | |
| C. | 图象M关于点(-$\frac{π}{12}$,0)对称 | |
| D. | f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{12}$)上递增 |
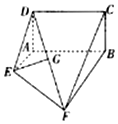 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.