题目内容
9.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a,b,c成等差数列,且sinA+sinC=$\sqrt{3}$.(Ⅰ)求角B的大小;
(Ⅱ)求4sinAcosC的取值范围.
分析 (Ⅰ)利用正弦定理把已知的等式化边为角,把C用π-(A+B)表示后整理求得B的值;
(Ⅱ)利用三角函数的积化和差变形,代入角B的值,然后根据A-C的范围得答案.
解答 解:(Ⅰ)由a,b,c成等差数列,可得2b=a+c,sinA+sinC=$\sqrt{3}$,可得A+C>90°.
可得2b(sinA+sinC)=$\sqrt{3}$(a+c),
得4RsinB(sinA+AcosC)=2$\sqrt{3}$R(sinA+sinC),
即sinB=$\frac{\sqrt{3}}{2}$.
∵0°<B<180°,
∴B=60°;
(Ⅱ)∵B=60°,
∴4sinAcosC=2[sin(A+C)+sin(A-C)]
=2sin60°+2sin(A-C)
=$\sqrt{3}$+2sin(A-C).
由0°<A<120°,0°<C<120°,得
-120°<A-C<120°.
∴-1≤sin(A-C)≤1.
-2≤2sin(A-C)≤2.
∴sinAcosC的取值范围是:[$\sqrt{3}$-2,2+$\sqrt{3}$].
点评 本题考查了解三角形,训练了正弦定理的应用,考查了三角函数的积化和差公式,是中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14.已知函数f(x)是偶函数,且当x≥0时,f(x)=log2(x+1)-x2,则f(f(3))=( )
| A. | -7 | B. | -46 | C. | 7 | D. | 46 |
1.已知抛物线y2=4x的焦点为F,定点P(4,-2),在抛物线上找一点M,使得|PM|+|MF|最小,则点M的坐标为( )
| A. | (2,-2) | B. | (1,2) | C. | (1,-2) | D. | (-1,2) |
18.某单位有496名职工,其中青年人有271名,中年人有178名,老年人有47名,为了了解该单位职工身体状况,抽取一个容量为n的样本进行统计分析,如表是根据抽取的样本数据(均为整数,单位:分)制作的频率分布表:
(1)采用分层抽样,在青年人、中年人和老年人中应各抽取多少人?
(2)试根据表中数据完成频率分布表(直接填写在在表格中);
(3)若数据在区间[59.5,74.5)的职工的身体处于亚健康状态,试问该单位约有多少名职工处于亚健康状态?
频率分布表
(1)采用分层抽样,在青年人、中年人和老年人中应各抽取多少人?
(2)试根据表中数据完成频率分布表(直接填写在在表格中);
(3)若数据在区间[59.5,74.5)的职工的身体处于亚健康状态,试问该单位约有多少名职工处于亚健康状态?
频率分布表
| 分组 | 频数 | 频率 |
| (49.5,59.5) | 12 | 0.24 |
| (59.5,69.5) | 16 | 0.32 |
| (69.5,79.5) | 10 | |
| (79.5,89.5) | 0.16 | |
| (89.5,99.5) | ||
| 合计 |
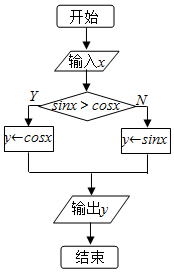 如图所示的流程图,若输出的x的值为$\frac{π}{3}$,则相应输出的y值为$\frac{1}{2}$.
如图所示的流程图,若输出的x的值为$\frac{π}{3}$,则相应输出的y值为$\frac{1}{2}$.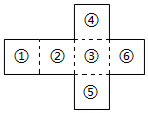 如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)
如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)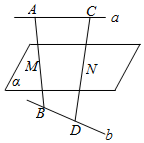 如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.
如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.