题目内容
4.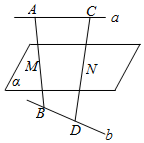 如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.
如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.
分析 连结AD交α于Q,连结MQ、NQ,则BD∥MQ AC∥NQ,由此结合已知条件能证明CN=DN.
解答  证明:连结AD交α于Q,连结MQ、NQ
证明:连结AD交α于Q,连结MQ、NQ
BD∥MQ,AC∥NQ,
∵AM=BM,∴M是AB中点,
∴Q也是AD中点,
∴N是CD中点,
∴CN=DN.
点评 本题考查两线段相等的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
16.已知角α的终边过点(sinθ,cosθ),则下列结论一定正确的是( )
| A. | α=θ | B. | α=θ+$\frac{π}{2}$ | C. | sin2θ+sin2α=1 | D. | sin2θ+cos2α=1 |
4.下列有关命题的说法正确的是( )
| A. | 若“p∧(?q)”为真命题,则“p∧q”也为真命题 | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| D. | 线性回归方程$\hat y=\hat bx+\hat a$对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 |
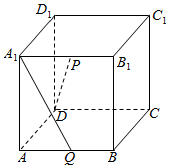 如图,在正方体ABCD-A1B1C1D1中,P是A1B1的中点,Q是AB的中点,求异面直线A1Q与DP所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,P是A1B1的中点,Q是AB的中点,求异面直线A1Q与DP所成角的余弦值.