题目内容
9.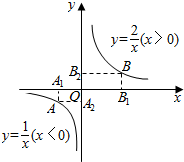 如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.
如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.
分析 先设A,B的坐标,求得|A2B2|=$\frac{2}{b}$-$\frac{1}{a}$=($\frac{2}{b}$-$\frac{1}{a}$)•1=$\frac{1}{4}$•($\frac{2}{b}$-$\frac{1}{a}$)•(b-a),展开后运用基本不等式求其最值.
解答 解:设A(a,$\frac{1}{a}$),B(b,$\frac{2}{b}$),(a<0,b>0),
由|A1B1|=4得,b-a=4,
而|A2B2|=$\frac{2}{b}$-$\frac{1}{a}$=($\frac{2}{b}$-$\frac{1}{a}$)•1
=$\frac{1}{4}$•($\frac{2}{b}$-$\frac{1}{a}$)•(b-a)
=$\frac{1}{4}$[3+(-$\frac{2a}{b}$)+(-$\frac{b}{a}$)]
≥$\frac{1}{4}$[3+2$\sqrt{(-\frac{2a}{b})•(-\frac{b}{a})}$]
=$\frac{3+2\sqrt{2}}{4}$,
即|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$,
当且仅当:b2=2a2,解得$\left\{\begin{array}{l}{a=4-4\sqrt{2}}\\{b=8-4\sqrt{2}}\end{array}\right.$,取“=”,
故答案为:$\frac{3+2\sqrt{2}}{4}$.
点评 本题主要考查了基本不等式在求最值问题中的应用,涉及“贴1法”的应用和对分析问题和解决问题能力的考查,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17.数列{an}满足a1=1,对任意的n∈N*都有an+1=a1+an+n,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2016}}}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{4034}{2017}$ |
4.已知全集U={1,2,3,4,5},集合M={3,4,5},N={1,2,5},则集合(∁UM)∩N可以表示为( )
| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
14.若△ABC的面积S△ABC∈[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$],且$\overrightarrow{AB}$•$\overrightarrow{BC}$=3,则向量$\overrightarrow{BA}$与$\overrightarrow{BC}$夹角的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{3π}{4}$,$\frac{5π}{6}$] | C. | [$\frac{2π}{3}$,π) | D. | [$\frac{2π}{3}$,$\frac{5π}{6}$] |
1.下列函数中值域为[0,+∞)的是( )
| A. | y=3x | B. | y=|x| | C. | y=x2-6x+7 | D. | $y=\frac{8}{x}$ |
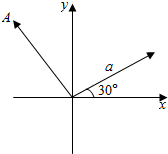 如图,点A的坐标为(-2,3),向量$\overrightarrow{a}$的模为4,则向量$\overrightarrow{OA}$的坐标为(-2,3),向量$\overrightarrow{a}$的坐标为(2$\sqrt{3}$,2).
如图,点A的坐标为(-2,3),向量$\overrightarrow{a}$的模为4,则向量$\overrightarrow{OA}$的坐标为(-2,3),向量$\overrightarrow{a}$的坐标为(2$\sqrt{3}$,2).