题目内容
18.方程log2(x-3)=log4(5-x)的解为4.分析 利用对数的运算性质变形,化为同底数后再转化为无理方程求解.
解答 解:由log2(x-3)=log4(5-x),得
$lo{g}_{2}(x-3)=\frac{1}{2}lo{g}_{2}(5-x)$,
∴$\left\{\begin{array}{l}{x-3>0}\\{5-x>0}\\{x-3=\sqrt{5-x}}\end{array}\right.$,解得:x=4.
∴方程log2(x-3)=log4(5-x)的解为:4.
故答案为:4.
点评 本题考查对数方程的解法,求解对数方程关键是注意验根,是基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
6.下列各组函数中,表示同一个函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=x,y=$\root{3}{{x}^{3}}$ | ||
| C. | y=$\sqrt{x-1}$×$\sqrt{x+1}$,y=$\sqrt{{x}^{2}-1}$ | D. | y=|x|,$y={({\sqrt{x}})^2}$ |
3.椭圆$\frac{x^2}{4}+{y^2}=1$的焦点为F1,F2,点M在椭圆上,且M在以F1F2为直径的圆上,则M到y轴的距离为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |

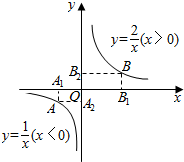 如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.
如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.