题目内容
17.数列{an}满足a1=1,对任意的n∈N*都有an+1=a1+an+n,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2016}}}}$=( )| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{4034}{2017}$ |
分析 利用累加法求出数列的通项公式,得到$\frac{1}{{a}_{n}}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$.再由裂项相消法求得答案.
解答 解:∵a1=1,
∴由an+1=a1+an+n,得
an+1-an=n+1,
则a2-a1=2,
a3-a2=3,
…
an-an-1=n(n≥2).
累加得:an=a1+2+3+…+n=$1+2+…+n=\frac{n(n+1)}{2}$(n≥2).
当n=1时,上式成立,
∴${a}_{n}=\frac{n(n+1)}{2}$.
则$\frac{1}{{a}_{n}}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2016}}}}$=2$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2016}-\frac{1}{2017})$=$2(1-\frac{1}{2017})=\frac{4032}{2017}$.
故选:C.
点评 本题考查数列递推式,考查了累加法求数列的通项公式,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
相关题目
12.已知f(x)=cos2x+2$\sqrt{3}$sinxcosx,则f($\frac{π}{12}$)=( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
2.已知不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$,构成平面区域Ω(其中x,y是变量),则目标函数z=3x+6y的最小值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
6.下列各组函数中,表示同一个函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=x,y=$\root{3}{{x}^{3}}$ | ||
| C. | y=$\sqrt{x-1}$×$\sqrt{x+1}$,y=$\sqrt{{x}^{2}-1}$ | D. | y=|x|,$y={({\sqrt{x}})^2}$ |

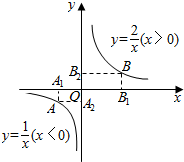 如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.
如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.