题目内容
已知函数f（x）=
，则不等式f（a2-4）＞f（3a）的解集为 ．
|
考点：函数单调性的性质,一元二次不等式的解法
专题：函数的性质及应用,不等式的解法及应用
分析：画出函数f（x）=
的图象，分析出函数的在R上为减函数，进而将原不等式化为a2-3a-4＜0，解二次不等式可得答案．
|
解答：
解：∵函数f（x）=
的图象如下图所示：
由图可得：函数f（x）=
在R上为减函数，
若f（a2-4）＞f（3a），
则a2-4＜3a，即a2-3a-4＜0，
解得：-1＜a＜4，
故不等式f（a2-4）＞f（3a）的解集为：（-1，4），
故答案为：（-1，4）
|
由图可得：函数f（x）=
|
若f（a2-4）＞f（3a），
则a2-4＜3a，即a2-3a-4＜0，
解得：-1＜a＜4，
故不等式f（a2-4）＞f（3a）的解集为：（-1，4），
故答案为：（-1，4）
点评：本题考查的知识点是函数单调性的性质，一元二次不等式的解法，其中判断出函数的在R上为减函数，是解答的关键．
练习册系列答案
相关题目
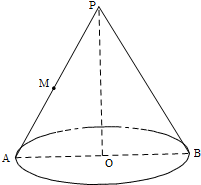已知圆锥母线长为6，底面圆半径长为4，点M是母线PA的中点，AB是底面圆的直径，底面半径OC与母线PB所成的角的大小等于θ．