题目内容
2.计算:${(\sqrt{2}•\root{3}{3})^6}-{log_2}({log_2}16)$=70.分析 利用有理数指数幂、对数性质和运算法则求解.
解答 解:${(\sqrt{2}•\root{3}{3})^6}-{log_2}({log_2}16)$
=${(\sqrt{2})^6}•{(\root{3}{3})^6}-{log_2}4$
=8×9-2=70.
故答案为:70.
点评 本题考查指数式、对数式化简求值,是基础题,解题时要 认真审题,注意有理数指数幂、对数性质和运算法则的合理运用.

练习册系列答案
相关题目
13.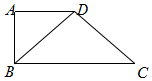 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
| A. | 面ABD⊥面ABC | B. | 面ADC⊥面BDC | C. | 面ABC⊥面BDC | D. | 面ADC⊥面ABC |
10.已知全集U={1,2,3,4},集合A={1,2},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {3} | C. | {1,3,4} | D. | {3,4} |
17.若函数f(x)=ex+e-x与g(x)=ex-e-x的定义域均为R,则( )
| A. | f(x)与g(x)与均为偶函数 | B. | f(x)为奇函数,g(x)为偶函数 | ||
| C. | f(x)与g(x)与均为奇函数 | D. | f(x)为偶函数,g(x)为奇函数 |
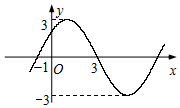 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.