题目内容
14.已知集合A={x|x2-3x-4≤0},B={x|x2-2mx+m2-9≤0},C={y|y=2x+b,x∈R}(1)若A∩B=[0,4],求实数m的值;
(2)若A∩C=∅,求实数b的取值范围;
(3)若A∪B=B,求实数m的取值范围.
分析 (1)求出A中不等式的解集确定出A,求出B中不等式解集表示出B,由A与B的交集确定出m的范围即可;
(2)由A与C的交集为空集,确定出b的范围即可;
(3)由A与B的并集为B,得到A为B的子集,确定出m的范围即可.
解答 解:(1)由A中不等式变形得:(x-4)(x+1)≤0,
解得:-1≤x≤4,即A=[-1,4];
由B中不等式变形得:(x-m+3)(x-m-3)≤0,
解得:m-3≤x≤m+3,即B=[m-3,m+3],
∵A∩B=[0,4],
∴$\left\{\begin{array}{l}{m-3=0}\\{m+3≥4}\end{array}\right.$,
解得:m=3;
(2)∵由C中y=2x+b>b,x∈R,得到C=(b,+∞),且A∩C=∅,A=[-1,4],
∴实数b的范围为b≥4;
(3)∵A∪B=B,
∴A⊆B,
∴$\left\{\begin{array}{l}{m-3≤-1}\\{4≤m+3}\end{array}\right.$,
解得:1≤m≤2.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
5.设$a={2016^{\frac{1}{2017}}},b={log_{2016}}^{\sqrt{2017}},c={log_{2017}}^{\sqrt{2016}}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>b>a |
9.已知偶函数f(x)在区间[0,+∞)单调递减,则满足 $f(2x-1)>f(\frac{1}{3})$的实数x的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
19.设A={4,5,6,7},B={x∈N|3≤x<6},则A∩B=( )
| A. | {4,5,6} | B. | {4,5} | C. | {3,4,5} | D. | {5,6,7} |
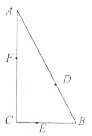 如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.
如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.