题目内容
设函数f（x）=
（1）求函数f（x）=
在点（3，2）处的导数；
（2）求与函数f（x）=
在点（3，2）处的切线垂直且经过切点的直线方程．
| x+1 |
| x-1 |
（1）求函数f（x）=
| x+1 |
| x-1 |
（2）求与函数f（x）=
| x+1 |
| x-1 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：（1）求出函数的导数，再令x=3，即可；
（2）运用两直线垂直的条件即斜率互为负倒数，求出所求直线的斜率，再由点斜式方程，求出所求直线的方程．
（2）运用两直线垂直的条件即斜率互为负倒数，求出所求直线的斜率，再由点斜式方程，求出所求直线的方程．
解答：
解：（1）∵函数f（x）=
，
∴f′（x）=
=
．
∴f′（3）=
=-
；
（2）∵切点为（3，2），切线的斜率为-
，
∴所求直线的斜率为2，
∴所求的直线方程为y-2=-2（x-3），即2x+y-8=0．
| x+1 |
| x-1 |
∴f′（x）=
| x-1-x-1 |
| (x-1)2 |
| -2 |
| (x-1)2 |
∴f′（3）=
| -2 |
| 4 |
| 1 |
| 2 |
（2）∵切点为（3，2），切线的斜率为-
| 1 |
| 2 |
∴所求直线的斜率为2，
∴所求的直线方程为y-2=-2（x-3），即2x+y-8=0．
点评：本题主要考查导数的运用：求切线，正确求出导数是解题的关键，同时考查两直线的位置关系：垂直．
练习册系列答案
相关题目
已知函数f（x）=cos（x+
）cosx（x∈R），则下面结论错误的是（ ）
| π |
| 2 |
| A、函数f（x）的最小正周期为π | ||
B、函数f（x）在区间[0，
| ||
C、函数f（x）的图象关于直线x=
| ||
| D、函数f（x）是奇函数 |
在数列{an}中，“n≥2，an=2an-1”是“{an}是公比为2的等比数列”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
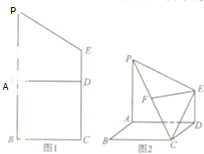如图1在梯形PBCE中，PB=2BC=4，CE=3，A是线段PB上一点，AD∥BC，现将四边形PADE沿AD折起，使得平面PADE⊥平面ABCD，连接PC，CE，得到如图2所示的空间图形，已知F是PC的中点，EF∥平面ABCD．