题目内容
设F1，F2是双曲线x2-
=1的左右焦点，O是原点，若双曲线右支上存在一点P满足：（
+
）•
=0，且|
|=λ|
|，则λ=（ ）
| y2 |
| 4 |
| OP |
| OF2 |
| F2P |
| PF1 |
| PF2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点：平面向量数量积的运算
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的方程求出焦点坐标F1、F2，离心率e；设出点P的坐标，由（
+
）•
=0以及双曲线的第二定义，求出|PF2|、|PF1|，即得λ的值．
| OP |
| OF2 |
| F2P |
解答：
解：由题意得，a=1，b=2，∴c=
，F1（-
，0），F2 （
，0），e=
；
设点P（
，m），
∵（
+
）•
=（
+
，m）•（
-
，m）=1+
-5+m2=0，
∴m2=
，∴m=±
；
由双曲线的第二定义得 e=
=
，∴|PF2|=2；
∴|PF1|=2a+|PF2|=4，
∴λ=
=
=2．
故选：C．
| 5 |
| 5 |
| 5 |
| 5 |
设点P（
1+
|
∵（
| OP |
| OF2 |
| F2P |
1+
|
| 5 |
1+
|
| 5 |
| m2 |
| 4 |
∴m2=
| 16 |
| 5 |
| 4 | ||
|
由双曲线的第二定义得 e=
| 5 |
| |PF2| | ||||||||
|
∴|PF1|=2a+|PF2|=4，
∴λ=
|
| ||
|
|
| 4 |
| 2 |
故选：C．
点评：本题考查了双曲线的标准方程以及几何性质的应用问题，解题时应熟练地掌握并能正确的应用这些知识，是中档题．
练习册系列答案
相关题目
已知函数f（x）=log
（3x2-ax+5）在[-1，+∞）上是减函数，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、-8≤a≤-6 |
| B、-8＜a＜-6 |
| C、-8＜a≤-6 |
| D、a≤-6 |
设集合U={（x，y）|x∈R，y∈R}，A={（x，y）|2x-y+m＞0}，B={（x，y）|x+y-n≤0}，若P（2，3）∈A∩（∁UB），则（ ）
| A、m＞-1且n＜5 |
| B、m＜-1且n＜5 |
| C、m＞-1且＞5 |
| D、m＜-1且n＞5 |
若可导函数f（x）图象过原点，且满足
=-1，则f′（0）=（ ）
| lim |
| △x→0 |
| f(△x) |
| △x |
| A、-2 | B、-1 | C、1 | D、2 |
给出四个函数图象分别满足：①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y）．
与如图函数图象对应的是（ ）
| A、①-a，②-b，③-c，④-d |
| B、①-b，②-c，③-a，④-d |
| C、①-a，②-c，③-b，④-d |
| D、①-d，②-a，③-b，④-c |
已知函数f（x）=cos（x+
）cosx（x∈R），则下面结论错误的是（ ）
| π |
| 2 |
| A、函数f（x）的最小正周期为π | ||
B、函数f（x）在区间[0，
| ||
C、函数f（x）的图象关于直线x=
| ||
| D、函数f（x）是奇函数 |
若b＜0＜a，d＜c＜0，则（ ）
| A、ac＞bd | ||||
B、
| ||||
| C、a-c＞b-d | ||||
| D、a-d＞b-c |
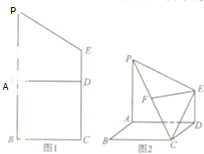如图1在梯形PBCE中，PB=2BC=4，CE=3，A是线段PB上一点，AD∥BC，现将四边形PADE沿AD折起，使得平面PADE⊥平面ABCD，连接PC，CE，得到如图2所示的空间图形，已知F是PC的中点，EF∥平面ABCD．