题目内容
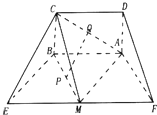 如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4| 2 |
| 2 |
(Ⅰ)求证:PQ∥平面BCE;
(Ⅱ)求证:AM⊥平面BCM;
(Ⅲ)求点F到平面BCE的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)根据AB∥EM,且AB=EM,推断出四边形ABEM为平行四边形,连接AE,则AE过点P,且P为AE中点,又Q为AC中点,进而可推断PQ是的中位线,可知PQ∥CE.最后根据线面平行的判定定理推断出PQ∥平面BCE.
(Ⅱ)AD⊥平面ABEF,推断出BC⊥平面ABEF,进而可知BC⊥AM,等腰梯形ABEF中由AF=BE=2,EF=4
,AB=2
可求得∠BEF,BM,进而可知AB2=AM2+BM2推断出AM⊥BM进而根据BC∩BM=B,推断出AM⊥平面BCM.
(Ⅲ)根据EM2=BE2+BM2,推断出MB⊥BE,又MB⊥BC,BC∩BE=B,根据线面垂直的判定定理推断出MB⊥平面BCE,进而根据d=2MB求得答案..
(Ⅱ)AD⊥平面ABEF,推断出BC⊥平面ABEF,进而可知BC⊥AM,等腰梯形ABEF中由AF=BE=2,EF=4
| 2 |
| 2 |
可求得∠BEF,BM,进而可知AB2=AM2+BM2推断出AM⊥BM进而根据BC∩BM=B,推断出AM⊥平面BCM.
(Ⅲ)根据EM2=BE2+BM2,推断出MB⊥BE,又MB⊥BC,BC∩BE=B,根据线面垂直的判定定理推断出MB⊥平面BCE,进而根据d=2MB求得答案..
解答:
证明:(Ⅰ)∵AB∥EM,且AB=EM,
∴四边形ABEM为平行四边形,
连接AE,则AE过点P,且P为AE中点,又Q为AC中点,
∴PQ是的中位线,于是PQ∥CE.
∵CE?平面BCE,PQ?平面BCE,
∴PQ∥平面BCE.
(Ⅱ)∵AD⊥平面ABEF,
∴BC⊥平面ABEF,
∴BC⊥AM
等腰梯形ABEF中由AF=BE=2,EF=4
,AB=2
可得∠BEF=45°,BM=AM=2,
∴AB2=AM2+BM2
∴AM⊥BM
又BC∩BM=B,∴AM⊥平面BCM.
(Ⅲ)点F到平面BCE的距离是M到平面BCE的距离的2倍,
∵EM2=BE2+BM2,
∴MB⊥BE,
又MB⊥BC,BC∩BE=B
∴MB⊥平面BCE,
∴d=2MB=4.
∴四边形ABEM为平行四边形,
连接AE,则AE过点P,且P为AE中点,又Q为AC中点,
∴PQ是的中位线,于是PQ∥CE.
∵CE?平面BCE,PQ?平面BCE,
∴PQ∥平面BCE.
(Ⅱ)∵AD⊥平面ABEF,
∴BC⊥平面ABEF,
∴BC⊥AM
等腰梯形ABEF中由AF=BE=2,EF=4
| 2 |
| 2 |
可得∠BEF=45°,BM=AM=2,
∴AB2=AM2+BM2
∴AM⊥BM
又BC∩BM=B,∴AM⊥平面BCM.
(Ⅲ)点F到平面BCE的距离是M到平面BCE的距离的2倍,
∵EM2=BE2+BM2,
∴MB⊥BE,
又MB⊥BC,BC∩BE=B
∴MB⊥平面BCE,
∴d=2MB=4.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用,点到面的距离.考查了学生基础知识的综合运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
若b<0<a,d<c<0,则( )
| A、ac>bd | ||||
B、
| ||||
| C、a-c>b-d | ||||
| D、a-d>b-c |
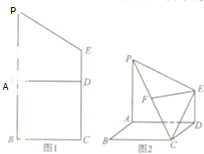 如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD.
如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD.