题目内容
调查某市出租车使用年限x和该年支出维修费用y（万元），得到数据如下：
则回归方程
=
x+
，必过定点（ ）
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 |
| y |
|
| b |
|
| a |
| A、（2，3） |
| B、（3，4） |
| C、（4，5） |
| D、（5，6） |
考点：线性回归方程
专题：概率与统计
分析：根据所给的数据，做出横标和纵标的平均数，写出样本中心点，根据线性回归方程一定过样本中心点，得到结果．
解答：
解：∵
=
=4，
=
=5，
∴这组数据的样本中心点是（4，5）
∵线性回归方程过样本中心点，
故选：C．
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2.2+3.8+5.5+6.5+7.0 |
| 5 |
∴这组数据的样本中心点是（4，5）
∵线性回归方程过样本中心点，
故选：C．
点评：本题考查线性回归方程，是一个基础题，题目中的运算量很小，若出现一定是一个送分题目，注意平均数不要出错．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数f（x）=log
（3x2-ax+5）在[-1，+∞）上是减函数，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、-8≤a≤-6 |
| B、-8＜a＜-6 |
| C、-8＜a≤-6 |
| D、a≤-6 |
已知函数f（x）=cos（x+
）cosx（x∈R），则下面结论错误的是（ ）
| π |
| 2 |
| A、函数f（x）的最小正周期为π | ||
B、函数f（x）在区间[0，
| ||
C、函数f（x）的图象关于直线x=
| ||
| D、函数f（x）是奇函数 |
若b＜0＜a，d＜c＜0，则（ ）
| A、ac＞bd | ||||
B、
| ||||
| C、a-c＞b-d | ||||
| D、a-d＞b-c |
已知数列{an}的前n项和Sn=2n2+3n-1，则a5的值为（ ）
| A、20 | B、21 | C、22 | D、23 |
已知直线l的方程：x-y-1=0，则直线l的倾斜角α=（ ）
| A、45° | B、60° |
| C、120° | D、135° |
在数列{an}中，“n≥2，an=2an-1”是“{an}是公比为2的等比数列”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
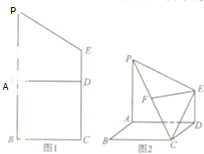如图1在梯形PBCE中，PB=2BC=4，CE=3，A是线段PB上一点，AD∥BC，现将四边形PADE沿AD折起，使得平面PADE⊥平面ABCD，连接PC，CE，得到如图2所示的空间图形，已知F是PC的中点，EF∥平面ABCD．