已知在△ABC中.c=6.A=120°.C=30°.解这个三角形．题目和参考答案——青夏教育精英家教网—

题目内容

10．已知在△ABC中，c=6，A=120°，C=30°，解这个三角形．

分析利用三角形的内角和得出B，由正弦定理得出a，b．

解答解：∵A=120°，C=30°，∴B=180°-120°-30°=30°，
∴B=C，
∴b=c=6，
由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$，即$\frac{a}{\frac{\sqrt{3}}{2}}=\frac{6}{\frac{1}{2}}$，
解得a=6$\sqrt{3}$．

点评本题考查了使用正弦定理解三角形，属于基础题．

练习册系列答案

成长记寒假总动员云南科技出版社系列答案

相关题目

20．

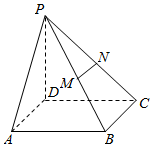如图，已知四棱锥P-ABCD，PD⊥底面ABCD，且底面ABCD是边长为2的正方形，M、N分别为PB、PC的中点．
（Ⅰ）证明：MN∥平面PAD；
（Ⅱ）若PA与平面ABCD所成的角为45°，求四棱锥P-ABCD的体积V．

1．已知集合A={x|y=$\sqrt{x-3}$}，B=（0，+∞），则A∩B=（　　）

18．

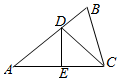如图，设△ABC的个内角A、B、C对应的三条边分别为a、b、c，且角A、B、C成等差数列，a=2，线段AC的垂直平分线分别交线段AB、AC于D、E两点．
（1）若△BCD的面积为$\frac{\sqrt{3}}{3}$，求线段CD的长；
（2）若DE=$\frac{\sqrt{6}}{2}$，求角A的值．

5．在△ABC中，若A=45°，B=60°，则$\frac{a-b}{a+b}$=2$\sqrt{6}$-5．

15．过抛物线y²=4x的焦点F作直线l，与抛物线分别交于A、B两点（A点在第一象限），若S_△AOB=3S_△FOB，则直线l的斜率k=（　　）

2．设N是自然数集，P={x|y=$\sqrt{3x-{x}^{2}}$，则集合P∩N中元素个数是（　　）

19．设x∈（0，$\frac{π}{2}$]，则下列命题：（1）x≥sinx；（2）sinx≥xcosx；（3）y=$\frac{sinx}{x}$是单调减函数，其中真命题的个数是（　　）

20．若存在实数x，y同时满足x²+y²≤1，|x-a|+|y-1|≤1，则实数a的取值范围是[-$\sqrt{2}$，$\sqrt{2}$]．

试题分类