题目内容
20.若存在实数x,y同时满足x2+y2≤1,|x-a|+|y-1|≤1,则实数a的取值范围是[-$\sqrt{2}$,$\sqrt{2}$].分析 化简不等式组,作出对应的图象,结合直线和圆相切的条件求出对应的a的值即可得到结论.
解答 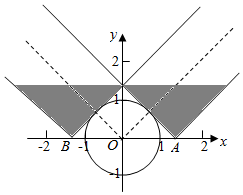 解:∵存在实数x,y同时满足x2+y2≤1,|x-a|+|y-1|≤1,
解:∵存在实数x,y同时满足x2+y2≤1,|x-a|+|y-1|≤1,
则-1≤y≤1,
则不等式,|x-a|+|y-1|≤1等价|x-a|-y+1≤1,
即|x-a|≤y,
作出x2+y2≤1,|x-a|≤y,对应的区域如图,
当a<0,x>a直线方程为y=x-a,即x-y-a=0,
此时当直线x-y-a=0与圆相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{2}}$=1,即|a|=$\sqrt{2}$,
此时a=-$\sqrt{2}$,即此时B(-$\sqrt{2}$,0),
当a>0,x<a直线方程为y=-(x-a),即x+y-a=0,
此时当直线x+y-a=0与圆相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{2}}$=1,即|a|=$\sqrt{2}$,
此时a=$\sqrt{2}$,即此时A($\sqrt{2}$,0),
若存在实数x,y同时满足x2+y2≤1,|x-a|+|y-1|≤1,
则-$\sqrt{2}$≤a≤$\sqrt{2}$,
故答案为:[-$\sqrt{2}$,$\sqrt{2}$]
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
8.函数y=x2+2x-1的顶点坐标是( )
| A. | ($\frac{1}{10}$,2) | B. | ($\frac{1}{10}$,-2) | C. | (-1,-2) | D. | (1,-2) |