题目内容
20.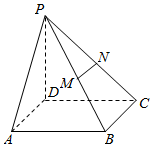 如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.(Ⅰ)证明:MN∥平面PAD;
(Ⅱ)若PA与平面ABCD所成的角为45°,求四棱锥P-ABCD的体积V.
分析 (I)由中位线定理得出MN∥BC,由MN∥AD,故MN∥AD,得出MN∥平面PAD;
(II)由∠PAD=45°得出PD=AD,于是棱锥体积V=$\frac{1}{3}{S}_{正方形ABCD}•PD$.
解答 (Ⅰ)证明:∵M、N分别是棱PB、PC中点,
∴MN∥BC,
又 ABCD是正方形,∵AD∥BC,
∴MN∥AD.
∵MN?平面PAD,AD?平面PAD,
∴MN∥平面PAD.
(Ⅱ)∵PD⊥平面ABCD,∴PA与平面ABCD所成的角为∠PAD,
∴∠PAD=45°.
∴PD=AD=2,
故四棱锥P-ABCD的体积V=$\frac{1}{3}{S}_{正方形ABCD}•PD$=$\frac{1}{3}×{2}^{2}×2=\frac{8}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
10.某单位为了制定节能减排的目标,先调查了用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
由表中数据,得线性回归方程$\widehaty=-2x+\widehata$,由此估计用电量为72度时气温的度数约为( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A. | -10 | B. | -8 | C. | -6 | D. | -4 |
8.“m>n>0”是“曲线mx2+ny2=1为焦点在x轴上的椭圆”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |