题目内容
2.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+2y+1≥0}\\{2x+y-1≤0}\end{array}\right.$,若直线y=k(x+1)把不等式组表示的平面区域分成上、下两部分的面积比为1:2,则k=$\frac{1}{4}$.分析 作出不等式组对应的平面区域,根据面积比是1:2,即可确定k的值
解答 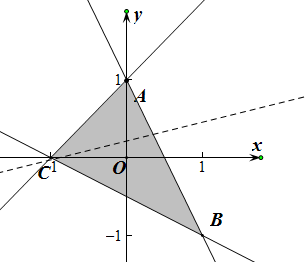 解:作出不等式组对应平面区如图(三角形ABC部分),A(0,1),B(1,-1),
解:作出不等式组对应平面区如图(三角形ABC部分),A(0,1),B(1,-1),
∵直线y=k(x+1)过定点C(-1,0),
∴C点在平面区域ABC内,
∴点A到直线y=k(x+1)的距离d上=$\frac{|k-1|}{\sqrt{1+{k}^{2}}}$,
点B到直线y=k(x+1)的距离d下=$\frac{|2k+1|}{\sqrt{1+{k}^{2}}}$,
∵直线y=k(x+1)把不等式组表示的平面区域分成上、下两部分的面积比为1:2,
∴2×$\frac{|k-1|}{\sqrt{1+{k}^{2}}}$=$\frac{|2k+1|}{\sqrt{1+{k}^{2}}}$,
解得k=$\frac{1}{4}$;
故答案为:$\frac{1}{4}$
点评 本题主要考查二元一次不等式组表示平面区域以及三角形的面积的应用,利用数形结合是解决本题的关键

练习册系列答案
相关题目
13.若3sinα-4cosα=5,则tan(α+$\frac{π}{4}$)=( )
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
14.若$cos(π-α)=\frac{4}{5}$,α是第三象限的角,则$sin(α+\frac{π}{4})$等于( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
11.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 0 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
14.四棱锥P-ABCD的底面ABCD为平行四边形,且AB=2,BC=1,AC=2,记平面PAD与平面PBC的交线为m,平面PAB与平面PDC的交线为n,则m与n所成的锐角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{32}$ | D. | $\frac{7}{8}$ |
11.设a,b,c∈R,且a>b,则( )
| A. | a2>b2 | B. | a3>b3 | C. | $\frac{1}{a}$$<\frac{1}{b}$ | D. | ac>bc |