题目内容
已知全集U=R,集合A={x|y=ln(3x-1)},B={y|y=sin(x+2)},则(∁UA)∩B=( )
A、(
| ||
B、(0,
| ||
C、[-1,
| ||
| D、∅ |
考点:交、并、补集的混合运算
专题:集合
分析:求出A中x的范围确定出A,求出B中y的范围确定出B,根据全集U=R求出A的补集,找出A补集与B的交集即可.
解答:
解:由A中y=ln(3x-1),
得到3x-1>0,即x>
,
∴A=(
,+∞),
∵全集U=R,
∴∁UA=(-∞,
],
由B中y=sin(x+2),得到-1≤y≤1,
∴B=[-1,1],
则(∁UA)∩B=[-1,
].
故选:C.
得到3x-1>0,即x>
| 1 |
| 3 |
∴A=(
| 1 |
| 3 |
∵全集U=R,
∴∁UA=(-∞,
| 1 |
| 3 |
由B中y=sin(x+2),得到-1≤y≤1,
∴B=[-1,1],
则(∁UA)∩B=[-1,
| 1 |
| 3 |
故选:C.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
若复数Z=a2-1+(a-1)i(其中a∈R)为纯虚数,则复数
在复平面内对应的点位于( )
| 1+ai |
| 2+3i |
| A、第二或第三象限 |
| B、第三或第四象限 |
| C、第三象限 |
| D、第四象限 |
已知函数f(x)=
,若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
|
| A、e | ||
B、
| ||
| C、e2 | ||
D、
|
在三角形ABC中,a=2,A=30°,C=45°,则三角形的面积S的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知函数f(x)=2x-1-log
x,则f(x)的零点的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |

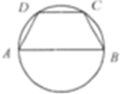 如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为
如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为