Question

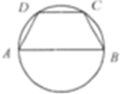如图，已知AB=2c（2c为常数且c＞0）．以AB为直径的圆有一内接梯形ABCD，且AB∥CD．若椭圆以A、B为焦点．且过C、D两点，则当梯形ABCD的面积最大时，椭圆的离心率为

 

．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：设∠BAC=θ，作CE⊥AB于点E，则可表示出BC，EB，CD，进而可求得梯形的面积的表达式，根据二次函数的性质求得面积的最大值时θ的值，则AC和BC可求，进而根据椭圆的定义求得椭圆的长轴，利用离心率公式，可得结论．

解答： 解：设∠BAC=θ，过C作CE⊥AB，垂足为E，则
BC=2csinθ，CE=BCsin（90°-θ）=2csin2θ，
∴CD=2c-4csin2θ，
梯形的面积S=

1

2

•（DC+AB）•CE=

1

2

•2csin2θ（2c+2c-4csin2θ）=4c（-sin²2θ+sin2θ），当sin2θ=

1

2

时，面积有最大值，
此时θ=30°，则BC=c，AC=

3

c，a=

1

2

（AC+BC）=

3 +1

2

•c，e=

c

a

=

c

3 +1 2 •c

=

3

-1．
故答案为：

3

-1

点评：本题主要考查了椭圆的应用，考查椭圆与圆的综合，考查椭圆的几何性质，充分利用了椭圆的定义．