题目内容
已知0<b<1,lga+lgb=0,实数x,y满足loga
=|x|,则y关于x的函数的图象大致是( )
| 1 |
| y |
A、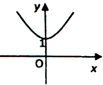 |
B、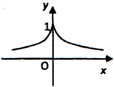 |
C、 |
D、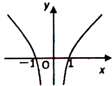 |
考点:函数的图象
专题:函数的性质及应用
分析:先化简函数的解析式,函数中含有绝对值,故可去绝对值讨论,当x≥0时,f(x)=(
)x=(b)|x|,结合已知分析出0<b<1,此时函数为减函数,又因为f(x)为偶函数,故可选出答案.
| 1 |
| a |
解答:
解:∵lga+lgb=lg(ab)=0,
故ab=1,即b=
,
∵loga
=|x|,
∴y=(
)|x|=(b)|x|
当x≥0时,f(x)=(b)x,
∵0<b<1,故此时函数为减函数,
又因为f(x)为偶函数,图象关于y轴对称,
故选B.
故ab=1,即b=
| 1 |
| a |
∵loga
| 1 |
| y |
∴y=(
| 1 |
| a |
当x≥0时,f(x)=(b)x,
∵0<b<1,故此时函数为减函数,
又因为f(x)为偶函数,图象关于y轴对称,
故选B.
点评:本题考查指数函数的图象问题、考查识图能力,属于基础题.

练习册系列答案
相关题目
如图,在复平面中,复数z1、z2分别对应点A、B,则|z1|•
=( )

. |
| z2 |

A、2
| ||||
B、2
| ||||
| C、3-i | ||||
| D、4+3i |
二项式(x+1)8(x-1)展开式中x5的系数是( )
| A、-14 | B、14 |
| C、-28 | D、28 |
若0<α<π,tan(π-α)=
,则cosα=( )
| 4 |
| 3 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知全集U=R,集合A={x|y=ln(3x-1)},B={y|y=sin(x+2)},则(∁UA)∩B=( )
A、(
| ||
B、(0,
| ||
C、[-1,
| ||
| D、∅ |
 已知有一个公园的形状如图所示,现有3种不同的植物药种在此公园的A,B,C,D,E这五个区域内,要求有公共边的两块相邻区域不同的植物,则不同的种法共有( )
已知有一个公园的形状如图所示,现有3种不同的植物药种在此公园的A,B,C,D,E这五个区域内,要求有公共边的两块相邻区域不同的植物,则不同的种法共有( )| A、16种 | B、18种 |
| C、20种 | D、22种 |
设f(n)=(
)n(n∈N*,i为虚数单位),则集合{x|x=f(n)}中元素的个数是( )
| 1+i |
| 1-i |
| A、1 | B、2 | C、3 | D、4 |