题目内容
某班从6名班干部(其中男生4人,女生2人)中,任选3人参加学校的义务劳动.
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(A|B).
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(A|B).
考点:条件概率与独立事件,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(1)求出总的选法、男生甲或女生乙被选中的选法,由此能求出男生甲或女生乙被选中的概率.
(2)求出女生乙被选中的概率、男生甲、女生乙都被选中的概率,即可得出结论.
(2)求出女生乙被选中的概率、男生甲、女生乙都被选中的概率,即可得出结论.
解答:
解:(1)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动,
总的选法有
=20种,男生甲或女生乙被选中的选法有
+
=12+4=16种,
∴男生甲或女生乙被选中的概率为
=
:
(2)总的选法有
=20种,女生乙被选中的概率为P(B)=
=
,
男生甲、女生乙都被选中的概率为P(AB)=
=
;
则在女生乙被选中下,男生甲被选中的概率为P(A|B)=
=
.
总的选法有
| C | 3 6 |
| C | 1 2 |
| C | 2 4 |
| C | 2 2 |
| C | 1 4 |
∴男生甲或女生乙被选中的概率为
| 16 |
| 20 |
| 4 |
| 5 |
(2)总的选法有
| C | 3 6 |
| ||
| 20 |
| 1 |
| 2 |
男生甲、女生乙都被选中的概率为P(AB)=
| ||
| 20 |
| 1 |
| 5 |
则在女生乙被选中下,男生甲被选中的概率为P(A|B)=
| P(AB) |
| P(B) |
| 2 |
| 5 |
点评:本题着重考查了随机事件的概率和条件概率公式等知识,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
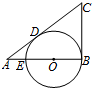 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为