题目内容
已知a＞0，b＞0，函数f（x）=|x+a|+|x-b|的最小值为2，则a2+b2的最小值为 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由条件利用绝对值的意义可得b+a=2，利用基本不等式求得ab≤1，再根据a2+b2 =（a+b）2-2ab=4-2ab求得a2+b2的最小值．
解答：
解：∵a＞0，b＞0，∴f（x）=|x+a|+|x-b|≥|x+a-（x-b）|=a+b=2，
由基本不等式可得2=a+b≥2
，∴ab≤1，当且仅当a=b时，等号成立．
a2+b2 =（a+b）2-2ab=4-2ab≥22-2=2，
故答案为：2．
由基本不等式可得2=a+b≥2
| ab |
a2+b2 =（a+b）2-2ab=4-2ab≥22-2=2，
故答案为：2．
点评：本题主要考查绝对值的几何意义，基本不等式的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
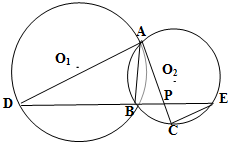如图所示，已知⊙O1与⊙O2相交于A，B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1，⊙O2于点D，E，DE与AC相交于点P．若AD是⊙O2的切线，且PA=6，PC=2，BD=9，AB的长为