题目内容
已知函数f(x)在其定义域x∈[0,+∞)时单调递增,且对任意的x,y∈[0,+∞)都有f(x+y)=f(x)+f(y)+1成立,且f(1)=2,
(1)求f(0),f(3)的值;
(2)解不等式:f(2x)+f(x-1)>7.
(1)求f(0),f(3)的值;
(2)解不等式:f(2x)+f(x-1)>7.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)利用赋值法即可求f(0),f(3)的值,
(2)若f(1)=2,结合抽象函数将不等式f(2x)+f(x-1)>7进行转化,结合函数的单调性解不等式即可.
(2)若f(1)=2,结合抽象函数将不等式f(2x)+f(x-1)>7进行转化,结合函数的单调性解不等式即可.
解答:
解:(1)∵f(x+y)=f(x)+f(y)+1成立,且f(1)=2,
∴令x=1,y=0得f(1)=f(1)+f(0)+1,
则f(0)=-1;
f(2)=f(1+1)=f(1)+f(1)+1=5,
f(3)=f(1+2)=f(1)+f(2)+1=2+5+1=8.
(2)由f(2x)+f(x-1)>7得:f(2x)+f(x-1)+1>7+1=f(3),
即f(3x-1)>f(3),
∵f(x)在其定义域x∈[0,+∞)时单调递增,
∴
⇒x>
.
故不等式的解集为(
,+∞)
∴令x=1,y=0得f(1)=f(1)+f(0)+1,
则f(0)=-1;
f(2)=f(1+1)=f(1)+f(1)+1=5,
f(3)=f(1+2)=f(1)+f(2)+1=2+5+1=8.
(2)由f(2x)+f(x-1)>7得:f(2x)+f(x-1)+1>7+1=f(3),
即f(3x-1)>f(3),
∵f(x)在其定义域x∈[0,+∞)时单调递增,
∴
|
| 4 |
| 3 |
故不等式的解集为(
| 4 |
| 3 |
点评:本题主要考查抽象函数的应用,根据函数单调性将不等式进行转化是解决本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
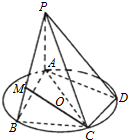 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,