题目内容
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB=2AD，BD=| 3 |
（1）求证：PA∥平面BMD；
（2）求证：AD⊥PB．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连接AC，AC与BD相交于点O，连接MO，先证明出MO∥AP，利用线面平行的判定定理证明出PA∥平面BMD．
（2）先根据线面垂直的性质证明出PD⊥AD，利用勾股定理证明出AD⊥BD，进而根据线面垂直的判定定理证明出AD⊥平面PBD，则AD⊥PB得证．
（2）先根据线面垂直的性质证明出PD⊥AD，利用勾股定理证明出AD⊥BD，进而根据线面垂直的判定定理证明出AD⊥平面PBD，则AD⊥PB得证．
解答：
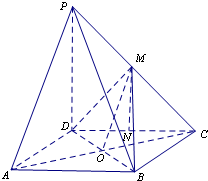（1）证明：连接AC，AC与BD相交于点O，连接MO，
∵ABCD是平行四边形，
∴O是AC的中点．
∵M为PC的中点，
∴MO∥AP．
∵P?平面BMD，MO?平面BMD，
∴PA∥平面BMD．
（2）证明：∵PD⊥平面ABCD，AD?平面ABCD，
∴PD⊥AD．
∵AB=2AD，BD=
AD
∴BD2+AD2=4AD2=AB2，
∴AD⊥BD．
∵PD∩BD=D，PD?平面PBD，BD?平面PBD，
∴AD⊥平面PBD．
∵PB?平面PBD，∴AD⊥PB．
（1）证明：连接AC，AC与BD相交于点O，连接MO，∵ABCD是平行四边形，
∴O是AC的中点．
∵M为PC的中点，
∴MO∥AP．
∵P?平面BMD，MO?平面BMD，
∴PA∥平面BMD．
（2）证明：∵PD⊥平面ABCD，AD?平面ABCD，
∴PD⊥AD．
∵AB=2AD，BD=
| 3 |
∴BD2+AD2=4AD2=AB2，
∴AD⊥BD．
∵PD∩BD=D，PD?平面PBD，BD?平面PBD，
∴AD⊥平面PBD．
∵PB?平面PBD，∴AD⊥PB．
点评：本题主要考查了线面平行，线面垂直的判定．考查了学生对立体几何基础知识的掌握．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
已知正项数列{an}中，a1=1，a2=2，2an2=an+12+an-12（n≥2），则a22等于（ ）
| A、16 | ||
| B、8 | ||
C、2
| ||
| D、4 |
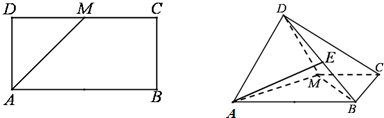如图，已知矩形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．
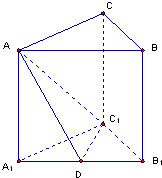如图，直三棱柱ABC-A1B1C1底面是等腰三角形（侧棱垂直于底面的棱柱叫直棱柱），A1C1=C1B1，D是线段A1B1的中点．