题目内容
已知函数f(x)=2sin(ωx),其中常数ω>0.
(Ⅰ)令ω=1,求函数F(x)=f(x)+f(x-
)的单调递增区间;
(Ⅱ)令ω=2,将函数y=f(x)的图象向左平移
个单位,再往上平移1个单位,得到函数y=g(x)的图象.若函数y=g(x)在区间[m,10π]上有20个零点:a1,a2,a3,…,a20,求实数m的取值范围并求a1+a2+a3+…+a19+a20的值.
(Ⅰ)令ω=1,求函数F(x)=f(x)+f(x-
| π |
| 3 |
(Ⅱ)令ω=2,将函数y=f(x)的图象向左平移
| π |
| 6 |
考点:复合三角函数的单调性,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(I)当ω=1时,函数F(x)=2
sin(x-
),令 2kπ-
≤x-
≤2kπ+
,k∈z,求得x的范围,可得函数的递增区间.
(II)令g(x)=0,可得 sin(2x+
)=-
,求得x=kπ+
,或 x=kπ+
,k∈z.由题意可得区间[m,10π]恰好包含函数g(x)的10个周期,可得m∈(-
,
],a1+a2+a3+…+a19+a20=[
+(π+
)+(2π+
)+…+(9π+
)]+[
+(π+
)+(2π+
)+…+(9π+
)],计算求得结果.
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(II)令g(x)=0,可得 sin(2x+
| π |
| 3 |
| 1 |
| 2 |
| 5π |
| 12 |
| 3π |
| 4 |
| π |
| 4 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 5π |
| 12 |
解答:
解:(I)当ω=1时,函数F(x)=f(x)+f(x-
)=2sinx+2sin(x-
)=3sinx-
cosx=2
sin(x-
),
令 2kπ-
≤x-
≤2kπ+
,k∈z,求得 2kπ-
≤x≤2kπ+
,故函数的递增区间为 [2kπ-
,2kπ+
π],k∈Z.
(II)由题意可得 g(x)=2sin2(x+
)+1=2sin(2x+
)+1,令g(x)=0,可得 sin(2x+
)=-
,
2x+
=2kπ+
,或2x+
=2kπ+
,即 x=kπ+
,或 x=kπ+
,k∈z.
若函数y=g(x)在区间[m,10π]上有20个零点,则区间[m,10π]恰好包含10个周期,
函数在区间[m+kπ,m+(k+1)π]上恰有两个零点,故在[m,10π]上有20个零点.
∴m∈(-
,
],a1+a2+a3+…+a19+a20=[
+(π+
)+(2π+
)+…+(9π+
)]+[
+(π+
)+(2π+
)+…+(9π+
)]
=
+
=
.
| π |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
| π |
| 6 |
令 2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
(II)由题意可得 g(x)=2sin2(x+
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
2x+
| π |
| 3 |
| 7π |
| 6 |
| π |
| 3 |
| 11π |
| 6 |
| 5π |
| 12 |
| 3π |
| 4 |
若函数y=g(x)在区间[m,10π]上有20个零点,则区间[m,10π]恰好包含10个周期,
函数在区间[m+kπ,m+(k+1)π]上恰有两个零点,故在[m,10π]上有20个零点.
∴m∈(-
| π |
| 4 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
=
| 295π |
| 6 |
| 105π |
| 2 |
| 305π |
| 3 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换、函数的奇偶性、根的存在性及根的个数的判断,考查数形结合思想,结合图象分析是解决问题的关键,属于基础题.

练习册系列答案
相关题目
已知f(x)=
,则f(f(-1))=( )
|
| A、1 | B、0 | C、-1 | D、e |
 在椭圆中,过焦点且垂直于长轴的直线被椭圆截得的弦,叫做椭圆的通径.如图,已知椭圆
在椭圆中,过焦点且垂直于长轴的直线被椭圆截得的弦,叫做椭圆的通径.如图,已知椭圆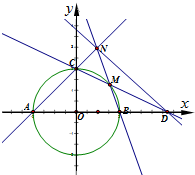 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C. 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD,BD=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD,BD=