题目内容
已知等比数列{an}通项式为an=(
)n,设bn=nan,求数列{bn}的前n项和Sn.
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:利用错位相减法求解.
解答:
解:∵an=(
)n,bn=nan,
∴bn=n•(
)n,
∴Sn=1•
+2•(
)2+3•(
)3+…+n•(
)n,①
Sn=1•(
)2+2•(
)3+3•(
)4+…+n•(
)n+1,②
①-②,得:
Sn=
+(
)2+(
)3+…+(
)n-n•(
)n+1
=
-n•(
)n+1
=1-(
)n-n•(
)n+1,
∴Sn=2-
.
| 1 |
| 2 |
∴bn=n•(
| 1 |
| 2 |
∴Sn=1•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②,得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||||
1-
|
| 1 |
| 2 |
=1-(
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=2-
| n+2 |
| 2n |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
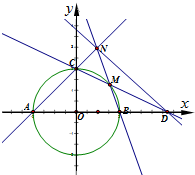 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C. 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD,BD=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD,BD= 20名学生某次数学考试成绩(单位:分)的频数分布直方图如图所示.
20名学生某次数学考试成绩(单位:分)的频数分布直方图如图所示.