题目内容
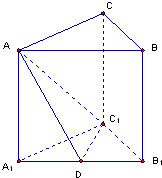如图，直三棱柱ABC-A1B1C1底面是等腰三角形（侧棱垂直于底面的棱柱叫直棱柱），A1C1=C1B1，D是线段A1B1的中点．（1）证明：面AC1D⊥平面A1B1BA；
（2）证明：B1C∥平面AC1D．
考点：直线与平面平行的判定,平面与平面垂直的判定
专题：空间位置关系与距离
分析：（1）先证明出C1D⊥平面A1B1BA，利用线面垂直的判定定理证明出面AC1D⊥平面A1B1BA．
（2）连结A1C交AC1于O，连结DO，先证明出DO∥B1C，根据线面平行的判定定理证明出B1C∥面AC1D．
（2）连结A1C交AC1于O，连结DO，先证明出DO∥B1C，根据线面平行的判定定理证明出B1C∥面AC1D．
解答：
证明：（1）∵面A1B1C1⊥面A1B1BA，面A1B1C1∩面A1B1BA=A1B1，C1D⊥A1B1，
∴C1D⊥平面A1B1BA，
∵C1D?面AC1D，
∴面AC1D⊥平面A1B1BA．
（2）连结A1C交AC1于O，连结DO，
∵D，O分别是A1B1，A1C的中点，
∴DO∥B1C，
∵DO?面AC1D，
∴B1C∥面AC1D．
∴C1D⊥平面A1B1BA，
∵C1D?面AC1D，
∴面AC1D⊥平面A1B1BA．
（2）连结A1C交AC1于O，连结DO，
∵D，O分别是A1B1，A1C的中点，
∴DO∥B1C，
∵DO?面AC1D，
∴B1C∥面AC1D．
点评：本题主要考查了线面平行，线面垂直的判定定理的应用．证明面面垂直的重要方法就是先找到线面垂直．
练习册系列答案
阅读快车系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB=2AD，BD=
20名学生某次数学考试成绩（单位：分）的频数分布直方图如图所示．