题目内容
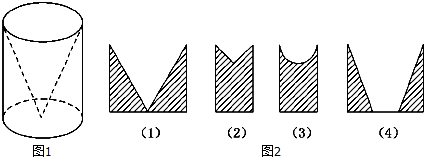
从如图1所示的圆柱中挖去一个以圆柱的上底面为底面，下底面的圆心为顶点的圆锥得到一个几何体，现用一个平面去截这个几何体，若这个平面垂直于圆柱的底面所在的平面，那么所截得的图形可能是图2中的 ．（把所有可能的图形的序号都填上）．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据圆锥曲线的定义和圆锥的几何特征，分截面过旋转轴时和截面不过旋转轴时两种情况，分析截面图形的形状，最后综合讨论结果，可得答案．
解答：
解：当截面过旋转轴时，
圆锥的轴截面为等腰三角形，此时（1）符合条件；
当截面不过旋转轴时，
圆锥的轴截面为双曲线的一支，此时（3）符合条件；
故截面图形可能是（1）（3），
故（1）（3）
圆锥的轴截面为等腰三角形，此时（1）符合条件；
当截面不过旋转轴时，
圆锥的轴截面为双曲线的一支，此时（3）符合条件；
故截面图形可能是（1）（3），
故（1）（3）
点评：本题考查的知识点是旋转体，圆锥曲线的定义，熟练掌握圆锥曲线的定义是解答的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
若a，b，c，d是空间四条直线．如果“a⊥c，b⊥c，a⊥d，b⊥d”，则（ ）
| A、a，b，c，d中任意两条可能都不平行 |
| B、a∥b |
| C、c∥d |
| D、a∥b或c∥d |