题目内容
若P为椭圆
+
=1上一点,F1、F2为焦点,∠F1PF2=60°,求P点坐标.
| x2 |
| 25 |
| y2 |
| 9 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知得S△F1PF2=9tan30°=3
,设P(x,y),则S△F1PF2=
|F1F2|•|y|=4|y|=3
,由此能求出P点坐标.
| 3 |
| 1 |
| 2 |
| 3 |
解答:
解:∵P为椭圆
+
=1上一点,F1、F2为焦点,∠F1PF2=60°,
∴S△F1PF2=9tan30°=3
,
设P(x,y),则S△F1PF2=
|F1F2|•|y|=4|y|=3
,
解得y2=
,∴x2=25-25×
=
,
∴P点坐标为(
,
),或(
,-
),或(-
,
),或(-
,-
).
| x2 |
| 25 |
| y2 |
| 9 |
∴S△F1PF2=9tan30°=3
| 3 |
设P(x,y),则S△F1PF2=
| 1 |
| 2 |
| 3 |
解得y2=
| 27 |
| 16 |
| ||
| 9 |
| 325 |
| 16 |
∴P点坐标为(
5
| ||
| 4 |
3
| ||
| 4 |
5
| ||
| 4 |
3
| ||
| 4 |
5
| ||
| 4 |
3
| ||
| 4 |
5
| ||
| 4 |
3
| ||
| 4 |
点评:本题考查椭圆上的点的坐标的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
过点A(7,2)作圆x2+y2+2x-4y-95=0的弦,则弦长的最大值和最小值之差为( )
| A、4 | B、6 | C、8 | D、12 |
函数f(x)=sin(ωx+
)(ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为
的等差数列,若要得到函数g(x)=sinωx的图象,只要将f(x)的图象( )个单位.
| π |
| 6 |
| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
两平行直线3x-4y-3=0和6x-8y+5=0之间的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则f[f(
)]=( )
|
| 1 |
| 2 |
| A、-1 | ||
| B、2 | ||
C、
| ||
D、
|
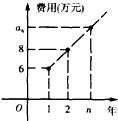 为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.
为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.