题目内容
已知偶函数f(x)=ax2+bx+c在点(1,1)处的切线与直线x+2y+9=0垂直,函数g(x)=f(x)+mln(x+1)(m≠0)
(1)求函数f(x)的解析式
(2)当m<
时,求函数g(x)的单调区间和极值点.
(1)求函数f(x)的解析式
(2)当m<
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:常规题型,导数的概念及应用
分析:第(1)问根据函数f(x)是偶函数,可以求出b,然后利用函数f(x)=ax2+bx+c在点(1,1)处的切线与直线x+2y+9=0垂直,可以构建a,c的方程组求出a,c;第(2)问在研究函数的单调性时要按方程g′(x)=0的根与定义域的关系分类讨论.
解答:
解:(1)因为f(x)偶函数,所以b=0,
因为f′(x)=2ax+b=2ax,由题意知:
,
解得
,所以f(x)=x2,…3分
(Ⅱ)g(x)=x2+mln(x+1),由题意知,g(x)的定义域为(-1,+∞),
g′(x)=2x+
=
当m<
时,x1=
,x2=
,
∵m<0时,x1=
<-1,x2=
>-1,
即x1∈(-∞,-1),x2∈(-1,+∞),
∴m<0时,g′(x),g(x)随x的变化情况如下表:
由表可知:m<0时,
函数g(x)的单调递增区间为(
,+∞),单调递减区间为(-1,
),
g(x)有唯一极小值点x =
,
当0<m<
时,x1=
>-1
∴x1,x2∈(-1,+∞)
此时,g′(x),g(x)随x的变化情况如下表:
由表可知:当0<m<
时,函数g(x)的单调递增区间为(-1,
),(
,+∞);
单调递减区间为(
,
),
函数g(x)的一个极大值点x=
和一个极小值点x=
,
综上所述:
m<0时,
函数g(x)的单调递增区间为(
,+∞),单调递减区间为(-1,
),
g(x)有唯一极小值点x =
,
0<m<
时,
函数g(x)的单调递增区间为(-1,
),(
,+∞);
单调递减区间为(
,
),
函数g(x)的一个极大值点x=
和一个极小值点x=
.
因为f′(x)=2ax+b=2ax,由题意知:
|
解得
|
(Ⅱ)g(x)=x2+mln(x+1),由题意知,g(x)的定义域为(-1,+∞),
g′(x)=2x+
| m |
| x+1 |
| 2x2+2x+m |
| x+1 |
当m<
| 1 |
| 2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∵m<0时,x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
即x1∈(-∞,-1),x2∈(-1,+∞),
∴m<0时,g′(x),g(x)随x的变化情况如下表:
| x | (-1,x2) | x2 | (x2,+∞) |
| g′(x) | - | 0 | + |
| g(x) | 减函数 | 极小值 | 增函数 |
函数g(x)的单调递增区间为(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
g(x)有唯一极小值点x =
-1+
| ||
| 2 |
当0<m<
| 1 |
| 2 |
-1-
| ||
| 2 |
∴x1,x2∈(-1,+∞)
此时,g′(x),g(x)随x的变化情况如下表:
| x | (-1,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
| 1 |
| 2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
单调递减区间为(
-1-
| ||
| 2 |
-1+
| ||
| 2 |
函数g(x)的一个极大值点x=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
综上所述:
m<0时,
函数g(x)的单调递增区间为(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
g(x)有唯一极小值点x =
-1+
| ||
| 2 |
0<m<
| 1 |
| 2 |
函数g(x)的单调递增区间为(-1,
-1-
| ||
| 2 |
-1+
| ||
| 2 |
单调递减区间为(
-1-
| ||
| 2 |
-1+
| ||
| 2 |
函数g(x)的一个极大值点x=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
点评:本题是利用导数研究函数的单调性、求函数的极值的基本题型,考查了分类讨论的思想,关键是抓住分类的标准.

练习册系列答案
相关题目
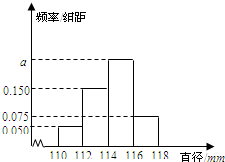 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.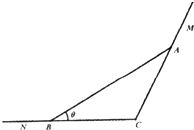 如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=
如图,用木板AB借助墙角MCN转成一个三角形ABC区域,用以堆放谷物,已知∠MCN=