题目内容
已知定义在R上的偶函数,并且满足f(x+2﹚=-
.
(1)当2≤x≤3时,f(x)=x,试求f(105.5)的值;
(2)当x∈[0,2]时,f(x)=2x-1 试求当x∈﹙6,10﹚时,f(x)的解析式.
| 1 |
| f(x) |
(1)当2≤x≤3时,f(x)=x,试求f(105.5)的值;
(2)当x∈[0,2]时,f(x)=2x-1 试求当x∈﹙6,10﹚时,f(x)的解析式.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数的奇偶性和条件,求出函数的周期性,利用周期性和奇偶性即可得到结论;
(2)利用函数的周期性即可求出函数f(x)的解析式.
(2)利用函数的周期性即可求出函数f(x)的解析式.
解答:
解:(1)∵f(x+2﹚=-
.
∴f(x+4)=f(x),即函数的周期是4.
则f(105.5)=f(4×26+1.5)=f(1.5),
∵f(x)是偶函数,∴f(1.5)=f(1.5-4)=f(-2.5)=f(2.5)=2.5,
故f(105.5)=f(1.5)=2.5.
(2)∵f(x)是偶函数,
∴当x∈[-2,0]时,-x∈[0,2],即f(-x)=2-x-1=f(x),即f(x)=2-x-1,
若x∈(6,8]时,x-8∈(-2,0],即f(x)=f(x-8)=28-x-1,
当x∈(8,10)时,x-8∈(0,2),即f(x)=f(x-8)=2x-8-1,
即f(x)=
.
| 1 |
| f(x) |
∴f(x+4)=f(x),即函数的周期是4.
则f(105.5)=f(4×26+1.5)=f(1.5),
∵f(x)是偶函数,∴f(1.5)=f(1.5-4)=f(-2.5)=f(2.5)=2.5,
故f(105.5)=f(1.5)=2.5.
(2)∵f(x)是偶函数,
∴当x∈[-2,0]时,-x∈[0,2],即f(-x)=2-x-1=f(x),即f(x)=2-x-1,
若x∈(6,8]时,x-8∈(-2,0],即f(x)=f(x-8)=28-x-1,
当x∈(8,10)时,x-8∈(0,2),即f(x)=f(x-8)=2x-8-1,
即f(x)=
|
点评:本题主要考查函数奇偶性和周期性的应用,根据条件求出函数的周期性是解决本题的关键.

练习册系列答案
相关题目
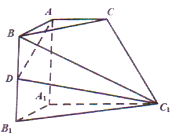 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.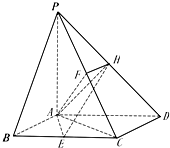 如图,四棱锥P-ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.
如图,四棱锥P-ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.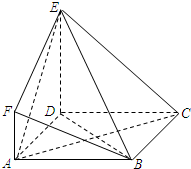 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为 如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱与底面垂直,点D是棱BC的中点.
如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱与底面垂直,点D是棱BC的中点.