Question

若曲线f（x，y）=0（或y=f（x））在其上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0（或y=f（x））的自公切线，下列方程的曲线存在自公切线的序号为

 

（写出所有满足题意的序号）
①y=3sinx+4cosx      
②x²-y²=1  
③y=x²-|x|
④|x|+1=

4-y2

．

Answer 1

考点：利用导数研究曲线上某点切线方程

专题：计算题,新定义

分析：①此函数是周期函数，过图象的最高点的切线都重合或过图象的最低点的切线都重合，故此函数有自公切线；
②x²-y²=1 是一个等轴双曲线，没有自公切线；
③去绝对值，配方，求出在x=±

1

2

处的切线，即可判断；
④先变形，再结合图象可得，此曲线没有自公切线．

解答： 解：①y=3sinx+4cosx=5sin（x+∅），cos∅=

3

5

，sin∅=

4

5

，此函数是周期函数，过图象的最高（或低）点的切线都重合，故此函数有自公切线；
 ②x²-y²=1 是一个等轴双曲线，没有自公切线；
③y=x²-|x|=

(x- 1 2 )2- 1 4 ，x≥0 (x+ 1 2 )2- 1 4 ，x＜0

在 x=

1

2

处和 x=--

1

2

处的切线都是y=-

1

4

，
故③有自公切线；
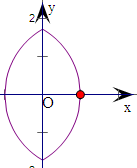
④|x|+1=

4-y2

即x²+2|x|+y²-3=0，结合图象可得，此函数没有自公切线．
故答案为：①③．

点评：本题考查函数的自公切线的定义，函数图象的特征，准确判断一个函数是否有自公切线，是解题的难点．